Chapter to appear in Simple heuristics that make us smart (Gigerenzer, G., Todd, P.M., and the ABC Research Group, in press; New York: Oxford University Press
Truth is ever to be found in simplicity, and not in the multiplicity and confusion of things. As the world, which to the naked eye exhibits the greatest variety of objects, appears very simple in its internal constitution when surveyed by a philosophical understanding, and so much the simpler by how much the better it is understood.
Isaac Newton
CHAPTER 1
Fast and Frugal Heuristics:
The Adaptive Toolbox
Gerd Gigerenzer and Peter M. Todd
A man is rushed to a hospital in the throes of a heart attack. The doctor needs to decide quickly whether the victim should be treated as a low risk or a high risk patient. He is at high risk if his life is truly threatened, and should receive the most expensive and detailed care. Although this decision can save or cost a life, the doctor does not have the luxury of extensive deliberation: She must decide under time pressure using only the available cues, each of which is, at best, merely an uncertain predictor of the patient’s risk level. For instance, at the University of California, San Diego Medical Center, as many as 19 such cues, including blood pressure and age, are measured as soon as a heart attack patient is admitted. Common sense dictates that the best way to make the decision is to look at the results of each of those measurements, rank them according to their importance, and combine them somehow into a final conclusion, preferably using some fancy statistical software package.
Consider in contrast the simple decision tree in Figure 1-1, which was designed by Breiman and colleagues (Breiman et al., 1993) to classify heart attack patients according to risk using only a maximum of three variables. If a patient has a systolic blood pressure of less than 91, he is immediately classified as high risk—no further information is needed. If not, then the decision is left to the second cue, age. If the patient is under 62.5 years old, he is classified as low risk; if he is older, then one more cue (sinus tachycardia) is needed to classify him as high or low risk. Thus, the tree requires the doctor to answer a maximum of three yes-no questions to reach a decision rather than to measure and consider 19 predictors, letting her proceed to life-saving treatment all the sooner.
[Figure 1-1]
This decision strategy is simple in several respects. First, it ignores the great majority of possible measured predictors. Second, it ignores quantitative information by using only yes/no answers to the three questions. For instance, it does not care how much older or younger the patient is than the 62.5 year cut-off. Third, the strategy is a step-by-step process; it may end after the first question and does not combine (e.g., weight and add) the values on the three predictors. Asking at most three yes-no questions is a fast and frugal strategy for making a decision. It is fast because it does not involve much computation, and it is frugal because it only searches for some of the available information. Its simplicity raises the suspicion that it might be highly inaccurate, compared to standard statistical classification methods that process and combine all available predictors. Yet it is actually more accurate in classifying heart attack patients according to risk status than are some rather complex statistical classification methods (Breiman et al., 1993). The more general form of this counterintuitive finding—that fast and frugal decision making can be as accurate as strategies that use all available information and expensive computation—forms one of the bases of our research program.
This book is about fast and frugal heuristics for
making decisions—how they work, and when and why they succeed. These heuristics
can be seen as models of the behavior of both living organisms and artificial
systems. From a descriptive standpoint, they are intended to capture how real
minds make decisions under constraints of limited time and knowledge. From an
engineering standpoint, these heuristics suggest ways to build artificially
intelligent systems—artificial decision-makers that are not paralyzed by the
need for vast amounts of knowledge or for extensive computational power. These
two applications of fast and frugal heuristics do not exclude one
another—indeed, the decision tree in Figure 1-1 could be used to describe the
behavior of an unaided human mind or could be built into an emergency-room
machine.[1]
Visions of Rationality:
From Demons to Bounded Rationality
Humans and animals make inferences about their world with limited time, knowledge, and computational power. In contrast, many models of rational inference view the mind as if it were a supernatural being possessing demonic powers of reason, boundless knowledge, and all of eternity with which to make decisions. Such visions of rationality often conflict with reality. But we can use them as points of comparison to help clarify our own vision of ecological rationality—rationality that is defined by its fit with reality. We start by considering two conceptual revolutions. The first is the demise of the dream of certainty and the rise of a calculus of uncertainty: that is, probability theory. This revolution is known as the probabilistic revolution in science and everyday life (Gigerenzer et al., 1989; Krüger et al., 1987). The second revolution, which this book is meant to advance, concerns how minds deal with an uncertain world. We propose replacing the image of an omniscient mind computing intricate probabilities and utilities, with that of a bounded mind reaching into an adaptive toolbox filled with fast and frugal heuristics.
Let us briefly sketch the first
revolution, as it concerns our views about mind and rationality. For two
millennia following Aristotle, the Western intellectual tradition distinguished
between two kinds of knowledge. One was demonstrative proof, the other probable
reasoning. The first provided certainty, while the second produced only
uncertain knowledge. During the Reformation and the Counter-Reformation of the
16th century, traditional sources of certainty—particularly religion and
philosophy—came under attack simultaneously. As a result, the domain of
demonstrative proof shriveled, while that of probable reasoning grew (Daston,
1988). By the mid-17th century, a new pragmatic rationality emerged that
abandoned traditional ideals of certainty. It was a modest view, expressed by
the calculus of probability invented during the same period. The modesty of
this vision stemmed from an acceptance that humble humans can attain only
uncertain knowledge about themselves and their world. To be rational, then,
required taming life’s uncertainty. Blaise Pascal’s (1669) famous wager
illustrates some moral consequences of this new rationality. In an atmosphere
of unwavering religious certainty that God had to exist, Pascal asked: Is it
rational to believe in Him? Pascal proposed that one should sacrifice worldly
pleasures to enhance one’s uncertain prospect of salvation, because no matter
how small the probability of God’s existence, the payoff of living a Christian
life is eternal afterlife, and the expected reward—the (perhaps small)
probability of salvation multiplied by its infinite value—is still infinite.
The other alternative—eternal damnation—was infinitely awful, no matter what
its probability. The new rationality expressed by the calculus of probability
was not just an intellectual revolution of thought, but also one in moral and
religious attitudes.
The probabilistic
revolution has shaped our picture of the mind in fields ranging from cognitive
science to economics to animal behavior. Mental functions are assumed to be
computations performed on probabilities and utilities (Gigerenzer & Murray,
1987). In this view, the laws of probability describe or prescribe sound
reasoning, judgment, and decision making. Probabilistic conceptions of the mind
have led to many elegant theories, but also to thorny problems. The moment one
moves beyond simple constrained settings such as ones that psychologists and
computer scientists study to real-world situations that people actually live
through, the time, knowledge, and computation that probabilistic models demand
grow unfeasibly large. As a consequence, when these models meet the rigors of
reality, they turn into a psychology more applicable to supernatural beings
than to mere humans.
In this book, we push for a second revolution, which provides a bold vision of rationality. Our premise is that much of human reasoning and decision making can be modeled by fast and frugal heuristics that make inferences with limited time and knowledge. These heuristics do not involve much computation, and do not compute probabilities and utilities. They are models of bounded rationality. This second theoretical upheaval embraces the earlier probabilistic revolution’s emphasis on uncertainty without sharing its focus on probability theory, either as a description or as an attainable norm of human behavior. The four major visions of rationality that continue to struggle with each other in this second upheaval are shown in Figure 1-2.
Rationality comes in many forms. The first split in Figure 1-2 separates models that assume the human mind has essentially unlimited demonic or supernatural reasoning power from those that assume we operate with only bounded rationality. There are two species of demons: those that exhibit unbounded rationality, and those that optimize under constraints. Unbounded rationality encompasses decision-making strategies that have little or no regard for the constraints of time, knowledge, and computational capacities that real humans face. Unbounded rationality is traditionally modeled by probability theory. Its best-known realizations are the maximization of expected utility and Bayesian models. There are also two main forms of bounded rationality: satisficing heuristics for searching through a sequence of available alternatives, and fast and frugal heuristics that use little information and computation to make a variety of kinds of decisions. We will illustrate these four conceptions of rationality by considering a commonly-faced decision problem, showing where the demons may lurk.
[Figure 1-2]
A couple of years after completing his historic scientific voyage on the Beagle, the 29-year-old Charles Darwin turned his mind to more domestic issues. He scrawled the following notes in pencil on a scrap of paper, divided into two columns like a balance sheet and headed “This is the Question”:
|
MARRY |
|
Not MARRY |
|
Children – (if it please God) – Constant companion, (& friend in old age) who will feel interested in one, object to be beloved and played with – better than a dog anyhow – Home, and someone to take care of house – Charms of music and female chit-chat. These things good for one’s health. Forced to visit and receive relations but terrible loss of time. My God, it is intolerable to think of spending one’s whole life, like a neuter bee, working, working, and nothing after all. – No, no won’t do. – Imagine living all one’s day solitary in smoky dirty London house. – Only picture to yourself nice soft wife on a sofa with good fire, and books and music perhaps – compare this vision with the dingy reality of Grt Marlboro’s St. |
|
No children, (no second life) no one to take care for one in old age.... Freedom to go where one liked – Choice of Society and little of it. Conversation of clever men at clubs – Not forced to visit relatives, and to bend in every trifle – to have the expense and anxiety of children – perhaps quarreling. Loss of time – cannot read in the evenings – fatness and idleness – anxiety and responsibility – less money for books etc – if many children forced to gain one’s bread. – (But then it is very bad for one’s health to work so much) Perhaps my wife won’t like London; then the sentence is banishment and degradation with indolent idle fool. |
(Darwin, 1969/1887, p. 232-233)
Darwin concluded that he should marry, writing “Marry – Marry – Marry Q. E. D” decisively beneath the first column. On the reverse side of the page he considered the consequences of his decision for his personal freedom, ending with the insight: “There is many a happy slave.” The following year, Darwin married his cousin, Emma Wedgwood, with whom he eventually had 10 children. How did Darwin decide to marry, based on the possible consequences he envisioned—children, loss of time, a constant companion? He did not tell us. But we can use his “Question” as a thought experiment to illustrate various visions of rationality.
Unbounded Rationality
When Darwin was just a 5-year-old child, dreamy and quiet and showing no signs of his later genius, the astronomer-philosopher Pierre Simon Laplace (1814) was contemplating the ultimate genius, an omniscient superintelligence he characterized as follows:
“Given ... an intelligence which could comprehend all the forces of which nature is animated and the respective situation of the beings who compose it—an intelligence sufficiently vast to submit these data to analysis ... nothing would be uncertain and the future, the past, would be present to its eyes” (Laplace, 1814, Essai Philosophique, p. 1325).
Laplace was areligious, and the superintelligence he imagined was a secularized version of God. John Locke (1690) had contrasted the omniscient God with us humble humans living in the “twilight of probability”; Laplace secularized this opposition with his fictitious superintelligence. From the perspective of God and Laplace’s superintelligence alike, Nature is deterministic and certain; but for humans, Nature is fickle and uncertain. Mortals cannot know the world, but must rely on uncertain inferences, on bets rather than on demonstrative proof. Although omniscience and certainty are not attainable for any real system, the spirit of Laplace’s superintelligence has survived nevertheless in the vision of unbounded rationality.
Imagine that Darwin had attempted to resolve his Question by maximizing his subjective expected utility. To compute his personal expected utility for marrying, he would have had to determine all the possible consequences that marriage could bring (e.g., children, constant companion, and an endless stream of further possibilities not included in his short list), attach quantitative probabilities to each of these consequences, estimate the subjective utility of each consequence, multiply each utility by its associated probability, and finally add all these numbers up. The same procedure would have to have been repeated for the alternative “not marry.” Finally, he would have had to choose the alternative with the higher total expected utility. To acquire reliable information about the consequences and their probabilities and utilities, Darwin might have had to invest years of research—time he could have spent studying barnacles or writing the Origin of Species.
Unbounded rationality is a strange and demanding
beast. On the one hand, researchers who envision rationality in this way accept
the difference between God, or Laplace’s superintelligence, and mere mortals.
Humans must make inferences from behind a veil of uncertainty, but Gods see
clearly; the currency of human thought is probabilities, whereas Gods deal in
certitude. On the other hand, when it comes to how they think these uncertain
inferences are executed, those who believe in unbounded rationality paint
humans in God’s image. God and Laplace’s superintelligence do not worry about
limited time, knowledge, or computational capacities. The fictional,
unboundedly rational human mind does not either—its only challenge is the lack
of heavenly certainty. In Figure 1-2, unbounded rationality appears in a class
of models of reasonableness labeled “demons.” We use the term in its original
Greek sense of a divine (rather than evil) supernatural being, as embodied in
Laplace’s superintelligence.
Proponents of unbounded rationality generally acknowledge that their models assume unrealistic mental abilities, but nevertheless defend them by arguing that humans act as if they were unboundedly rational. On this interpretation, the laws of probability do not describe the process but merely the outcome of reasoning. Another common defense is that this theory exhibits mathematical beauty and convenience. Finally, some proponents simply say, “don’t quarrel with success” (see Conslik, 1996; Selten, 1991).
The greatest weakness of unbounded rationality is
that it does not describe the way real people think. Not even philosophers, as
the following story illustrates. One philosopher was struggling to decide
whether to stay at Columbia University or to accept a job offer from a rival
university. The other advised him: “Just maximize your expected utility—you
always write about doing this.” Exasperated, the first philosopher responded:
“Come on, this is serious.”
Because of its unnaturalness, unbounded rationality has come under attack in the second half of the 20th century. But when one (unboundedly rational) head has been chopped off, another very similar one has usually sprouted again in its place: its close demonic relative, optimization under constraints.
Optimization Under Constraints
To think is to take a risk, a step into the unknown. Our inferences, inevitably grounded in uncertainty, force us to “go beyond the information given,” in Jerome Bruner’s famous phrase. But the situation is usually even more challenging than this, because rarely is information given. Instead we must search for information—cues to classify heart attack patients as high risk, reasons to marry, indicators of stock market fluctuation, and so on. Information search is usually thought of as being internal, performed on the contents of one’s memory. But it is important to recognize that much of information search is external, looking through the knowledge embodied in the surrounding environment. This external search includes seeking information in the socially distributed memory spanning friends and experts and in human artifacts such as libraries and the Internet.
The key difference between unbounded rationality and the three other visions in Figure 1-2 is that the latter all involve limited information search, whereas models of unbounded rationality assume that search can go on indefinitely. In reasonable models, search must be limited because real decision makers have only a finite amount of time, knowledge, attention, or money to spend on a particular decision. Limited search requires a way to decide when to stop looking for information, that is, a stopping rule. The models in the class we call “optimization under constraints” assume that the stopping rule optimizes search with respect to the time, computation, money, and other resources being spent. More specifically, this vision of rationality holds that the mind should calculate the benefits and costs of searching for each further piece of information and stop search as soon as the costs outweigh the benefits (e.g., Anderson & Milson, 1989; Sargent, 1993; Stigler, 1961). The rule “stop search when costs outweigh benefits” sounds plausible at first glance. But a closer look reveals that optimization under constraints can require even more knowledge and computation than unbounded rationality (Vriend, 1996; Winter, 1975).
To see this point, imagine the unboundedly rational
Darwin and a Darwin who optimizes under constraints, both of them trying to
decide whether or not to marry. The unboundedly rational Darwin has to search
for all the possible consequences of marrying and not marrying before choosing
the alternative with the higher subjective expected utility. Now suppose that
the Darwin who attempts to optimize under constraints has already listed two
consequences of marriage, having a constant companion and children, and
estimates of their respective probabilities and utilities. Before he proceeds
to a third consequence, he must calculate whether or not the benefits of
continuing the information search will outweigh its costs—if not, then he can
stop his search at this point. To compute the benefit of further search, this
poor Darwin would again have to consider what all the third consequences could
be, estimate their utilities and probabilities, calculate how much each one
could change his ultimate decision, and average all of these to come up with
the expected benefit of continuing his search. The same calculation has to be
performed before each further consequence is considered. Thus, calculating the
benefits of further search demands the same kind of knowledge that the
unboundedly rational Darwin needs. But the Darwin who tries to optimize under
constraints is not finished yet—he must also determine the costs of continuing
search. These include, for instance, the opportunity costs: The optimizing
Darwin must determine all the other things he could be doing during the time he
would be considering his decision (like dissecting another barnacle), and what
the cost of continuing to deliberate his Question instead of pursuing those
other activities would be. At the end, this leads to an infinite regress. The
optimizing Darwin would need to determine not only what the opportunity costs
are, but also the second-order costs for making all these cost-benefit
calculations, and so on (Conslik, 1996). Even the unboundedly rational Darwin
could make a decision faster than this.
Recall that the very motivation for replacing unbounded rationality by optimization under constraints was to build empirically more realistic models that respect the limitations of human minds. The paradoxical approach of optimization under constraints is to model “limited” search by assuming that the mind has essentially unlimited time and knowledge with which to evaluate the costs and benefits of further information search. The dream of optimization, threatened in its instantiation in unbounded rationality, is thus salvaged by being incorporated into an apparent competitor. When solving Darwin’s Question or other real-world problems, constrained optimization invites unbounded rationality to sneak in through the back door.
Of course, few would argue that real humans have the time and knowledge necessary to perform the massive computations required of either of these imaginary demonic Darwins. Instead, these visions of rationality are usually presented as lofty ideals that human reasoning should aspire to. But such aspirations make real human reasoning look flawed and irrational in comparison. In our view, it is these aspirations that are flawed—we will argue that reasoning can be powerful and accurate without requiring unlimited time and knowledge.
What certain forms of optimization under constraints
can offer—in contrast to unbounded rationality—is an analysis of the structure
of environments. For instance, in Anderson’s rational analysis framework
(Anderson, 1990; Oaksford & Chater, 1994) constraints from the environment,
rather than on the decision maker, are used to modify one’s understanding of
what is optimal behavior in a particular context. Such an analysis does not
directly address the question of what mental mechanisms could possibly yield
behavior approaching the optimal norm, but at least it allows us to create a
more realistic standard for assessing proposed mechanisms.
Instead of the demonic visions of reason, we turn to the idea of bounded rationality. Many, if not most, researchers in cognitive science, economics, and animal behavior interpret the term “bounded rationality” as synonymous with optimization under constraints, a (mis)use we strongly reject. This interpretation may be responsible for the frequent dismissal of bounded rationality in favor of good old-fashioned demonic visions. The economist Thomas Sargent (1993), for instance, in interpreting bounded rationality as constrained optimization, argues that when one models people as “bounded” in their rationality, one’s models use a greater number of parameters and become more demanding mathematically. He believes that the reason why researchers (particularly economists) stick with models incorporating unbounded rationality is that their desire for models with fewer parameters is not met by the bounded approach: “a reduction is not what bounded rationality promises” (p. 4). But this is a misleading interpretation of bounded rationality—rationality need not be optimization, and bounds need not be constraints.
Bounded Rationality: Satisficing
The “father” of bounded rationality, Herbert Simon, has vehemently rejected its reduction to optimization under constraints: “bounded rationality is not the study of optimization in relation to task environments” (Simon, 1991). In personal conversation, he once remarked with a mixture of humor and anger that he had considered suing authors who misuse his concept of bounded rationality to construct ever more complicated and unrealistic models of human decision making.
Simon’s vision of bounded rationality has two interlocking components: the limitations of the human mind, and the structure of the environments in which the mind operates. The first component of his vision means that models of human judgment and decision making should be built on what we actually know about the mind’s capacities rather than on fictitious competencies. In many real-world situations, optimal strategies are unknown or unknowable (Simon, 1987). Even in a game such as chess, where an optimal (best) move does in fact exist at every point, no strategy can calculate that move in a reasonable amount of time (either by human minds or computers), despite the well-defined nature of the possibilities to be searched. In less well-defined natural situations, our hope of identifying a useable optimal strategy is even further diminished. Because of the mind’s limitations, humans “must use approximate methods to handle most tasks” (Simon, 1990, p. 6). These methods include recognition processes that largely obviate the need for further information search, heuristics that guide search and determine when it should end, and simple decision rules that make use of the information found. We explore these classes of methods at length in this book.
The second component of Simon’s view of bounded
rationality, environmental structure, is of crucial importance because it can
explain when and why simple heuristics perform well: if the structure of the
heuristic is adapted to that of the environment. Simon’s (1956) classic example
concerns foraging organisms that have a single need, food. One organism lives
in an environment in which little heaps of food are randomly distributed; it
can get away with a simple heuristic, that is, run around randomly until a heap
of food is found. For this, the organism needs some capacity for vision and
movement, but it does not need a capacity for learning. A second organism lives
in an environment where food is not distributed randomly but comes in hidden
patches whose locations can be inferred from cues. This organism can use more
sophisticated strategies, such as learning the association between cues and
food, and a memory for storing this information. The general point is that in
order to understand which heuristics an organism employs, and when and why the
heuristic works well, one needs to look at the structure of the information in
the environment. Simon (1956) was not the only one to make this important point;
it was made both before his work (e.g., Brunswik, 1943) and at various times
since (e.g., Shepard, 1990; Anderson, 1990), including the extreme statement
only the environment need be studied, not the mechanisms of the mind (e.g.,
Gibson, 1979). But in general the second part of Simon’s (1956) paper title,
“Rational choice and the structure of environments,” has been neglected in
mainstream cognitive sciences (even by Simon himself—see Simon, 1987).
We use the term ecological rationality to bring environmental structure back into bounded rationality. A heuristic is ecologically rational to the degree that it is adapted to the structure of an environment (see below). Thus, simple heuristics and environmental structure can both work hand in hand to provide a realistic alternative to the ideal of optimization, whether unbounded or constrained.
One form of bounded rationality is Simon’s concept of satisficing—a word that originated in Northumbria (a province in England on the Scottish border), where it meant “to satisfy.” Satisficing is a method for making a choice from a set of alternatives encountered sequentially when one does not know much about the possibilities ahead of time. In such situations, there may be no optimal solution for when to stop searching for further alternatives—for instance, once Darwin decided to marry, there would be no optimal way of deciding when to stop looking for prospective marriage partners and settle down with a particular one (see Chapter 13 for more on satisficing in mate search). Satisficing takes the shortcut of setting an aspiration level and ending the search for alternatives as soon as one is encountered that exceeds the aspiration level (Simon, 1956a, 1990).
Satisficing is evident in the behavior of firefighter
commanders who make life-and-death decisions under extreme time pressure:
Rather than surveying all of the alternative courses of action to combat the
flames in, say, the basement of a four-story apartment building, they seem to
pick one possible action, play it quickly through in a mental simulation, and
if it works well enough—that is, if its outcome exceeds a predetermined
aspiration level for success—they act it out without ever considering other
alternatives. If the outcome of the mental simulation does not meet their
aspiration level, they go on to the next alternative, repeating the simulation
process until a satisfactory course of action is found (Klein, 1998).
Bounded Rationality: Fast and Frugal Heuristics
Satisficing is a way of making a decision about a set of alternatives that respects the limitations of human time and knowledge: it does not require finding out or guessing about all the options and consequences the future may hold, as constrained optimization does. However, some forms of satisficing can still require a large amount of deliberation on the part of the decision maker, for instance to set an appropriate aspiration level in the first place, or to calculate how a current option compares to the aspiration level (Simon, 1956b). Rather than let unrealistic mental computation slip back into our picture of human rationality, we narrow our focus still more to concentrate on fast and frugal heuristics for decision making.
Fast and frugal heuristics employ a minimum of time, knowledge, and computation to make adaptive choices in real environments. They can be used to solve problems of sequential search through objects or options, as in satisficing. They can also be used to make choices between simultaneously available objects, where the search for information (in the form of cues, features, consequences, etc.) about the possible options must be limited, rather than the search for the options themselves. Fast and frugal heuristics limit their search of objects or information using easily-computable stopping rules, and they make their choices with easily-computable decision rules. We thus see satisficing and fast and frugal heuristics as two overlapping but different categories of bounded rationality: there are some forms of satisficing that are fast and frugal, and others that are computationally unreasonable; and there are some fast and frugal heuristics that make satisficing sequential option decisions, and some that make simultaneous option choices. We consider fast and frugal heuristics to represent bounded rationality in its purest form.
How would a fast and frugal Darwin settle his marriage quandary? One way that he could make his decision between the two alternatives—to marry or not—with little time and knowledge would be to employ a form of one-reason decision making, in which he need only find a single piece of information to determine his decision. Indeed, the passage immediately before Darwin’s “Q. E. D.” can be read to suggest that there was only one decisive reason for his choice in favor of marriage, that of having a constant companion: “Imagine living all one’s day solitary in smoky dirty London house. Only picture to yourself nice soft wife on a sofa....” There is a sound reason why a person might base a decision on only one reason rather than on a combination of reasons: Combining information from different cues requires converting them into a common currency, a conversion that may be expensive if not actually impossible. For instance, to make his decision on the basis of several cues combined into one assessment of each option, Darwin would have to decide how many conversations with clever friends are equivalent to having one child, and how many hours in a smoky abode can be traded against a lifetime of soft moments on the sofa. Standard models of optimization, whether constrained or unbounded, assume that there is a common currency for all beliefs and desires, namely, quantitative probabilities and utilities. Although this is a mathematically convenient assumption, the way we look at the world does not always conform to it. Some things do not have a price tag, and cannot be reduced to and exchanged for any common currency (Elster, 1979). Love, true friendship, military honors, and Ph.D.’s, for example, are supposed to priceless, and therefore incommensurable with items for sale in a shopping mall. When reasons cannot be converted to a single currency, the mind has little choice but to rely on a fast and frugal strategy that bases its decision on just one good reason. As we will see, however, incommensurability is not the only reason for one-reason decision making (Chapters 4 - 6).
Before we take a closer look at fast and frugal
heuristics, let us sum up our discussion so far. Bounded rationality has become
a fashionable term in many quarters, and a plethora of proposed examples have
been thrown together under this term, including optimization under constraints.
Figure1-2 helps to make clear the distinctions between bounded rationality and
the demonic visions of rationality. Unbounded rationality is not concerned with
the costs of search, while bounded rationality explicitly limits search through
stopping rules. Optimization under constraints also limits search, but does so
by computing the optimal stopping point, that is, when the costs of further search
exceed the benefits. In contrast, bounded rationality “bets” on simple
heuristics for search and stopping rules that do not attempt to optimize.
Finally, the purest form of bounded rationality is to be found in fast and
frugal heuristics, which perform limited search through objects (in
satisficing) or cues and exploit environmental structure to yield adaptive
decisions.
The ABC’s of Fast and Frugal
Heuristics:
A New Research Program
This book promotes the view of bounded rationality as the way that real people make the majority of their inferences and decisions. It is also a useful framework for developing decision-making heuristics for artificial agents. The program of studying boundedly rational heuristics involves (a) designing computational models of candidate simple heuristics, (b) analyzing the environmental structures in which they perform well, (c) testing their performance in real-world environments, and (d) determining whether and when people really use these heuristics. The results of the investigatory stages (b), (c), and (d) can be used to inform the initial theorizing of stage (a). The different stages of this research program rest on multiple methods, including theoretical modeling of heuristics, computer simulation of their performance, mathematical analysis of the fit between heuristics and specific environments, and laboratory experimentation. We now consider each of the four stages in turn.
Computational Models
A computational model of a heuristic specifies the precise steps of information gathering and processing that are involved in generating a decision, such that the heuristic can be instantiated as a computer program. For a fast and frugal heuristic, this means the computational model must specify principles for guiding search for alternatives, information, or both, stopping that search, and making a decision.
Heuristic principles for guiding search. Decisions must be made between alternatives, and based on information about those alternatives. In different situations, those alternatives and pieces of information may need to be found through active search. The heuristic principles for guiding search, whether across alternatives or information, are what give search its direction (if it has one). For instance, search for cues can be simply random, or in order of some precomputed criterion related to their usefulness (see Chapter 6), or based on a recollection about which cues worked previously when making the same decision (see Chapter 4). Search for alternatives can similarly be random or ordered. Fast and frugal search-guiding principles do not use extensive computations or knowledge to figure out where to look next.
Heuristic principles for stopping search. In our conception of bounded rationality, the temporal limitations of the human mind (or that of any realistic decision-making agent) must be respected as much as any other constraints. This implies in particular that search for alternatives or information must be terminated at some point. Moreover, owing to the computational limitations of the human mind, the method for determining when to stop search should not be overly complicated. For example, one simple stopping rule is to cease searching for information and make a decision as soon as the first cue or reason that favors one alternative is found (see Chapter 4). This and other cue-based stopping rules do not need to compute an optimal cost-benefit trade-off as in optimization under constraints; in fact, they need not compute any costs or benefits at all. For alternative search, simple aspiration-level stopping rules can be used, as in Simon’s original satisficing notion (Simon, 1956, 1990; see also Chapter 13).
Heuristic principles for decision making. Once search has been guided to find the appropriate alternatives or information and then been stopped, a final set of heuristic principles can be called upon to make the decision or inference based on the results of the search. These principles can also be very simple and computationally bounded. For instance, a decision or inference can be based on only one cue or reason, whatever the total number of cues found during search (see Chapters 2 - 6). Such one-reason decision making does not need to weight or combine cues, and so no common currency between cues need be determined. Decisions can also be made through a simple elimination process, in which alternatives are thrown out by successive cues until only one final choice remains (see Chapters 8 and 11).
These heuristic principles are the building blocks, or the ABC’s, of fast and frugal heuristics. Given that the mind is a biological rather than a logical entity, formed through a process of successive accrual, borrowing, and refinement of components, it seems reasonable to assume that new heuristics are built from the parts of the old ones, rather than from scratch (Pinker, 1998; Wimsatt, 1998). In this light, we have used two main methods to construct computational models of fast and frugal heuristics: combining building blocks and nesting existing heuristics. Heuristic principles can be combined in multiple ways, such as the several guises in which we find one-reason decision making throughout this book, though of course not arbitrarily: For instance, fast and frugal heuristic for two-alternative choice that stops information search at the first cue on which the alternatives differ must also use a decision principle based on one-reason decision making. Whole fast and frugal heuristics can themselves be combined by nesting one inside another. As an example, the recognition heuristic (see Chapters 2 and 3) works on the basis of an elementary cognitive capacity, recognition memory, but it can also serve as the first step of heuristics that draw on other capacities, such as recall memory (see Chapters 4 and 5). Recognition memory develops earlier than recall memory both ontogenetically and evolutionarily, and the nesting of heuristics can similarly be seen as analogous to the addition of a new adaptation on top of an existing one.
We have formulated the fast and frugal heuristics in this book as precise step-by-step models that are highly transparent: it is easy to discern and understand just how they function to make decisions. Because they involve few free parameters and a minimum of computation, each step of the algorithm is open to scrutiny. These simple heuristics stand in sharp contrast to more complex and computationally involved models of mental processes, which may generate good approximations to human behavior but are also often rather opaque. For instance, the resurgence of connectionism in the 1980s brought forth a crop of neural networks that were respectable models for a variety of psychological phenomena, but whose inner workings remained mysterious even to their creators. Only with effort has the fascination with these black-box connectionist models been overcome, and new methods developed to allow us to see inside them (Regier, 1996; Rumelhart & Todd, 1993). The temptation of the black magic associated with black-box methods exists in other related domains, such as the use of complicated and opaque statistical packages to analyze behavior (Boyd & Richerson, 1985; Gigerenzer, 1993). Transparent models of fast and frugal heuristics avoid misunderstanding and mystification of the processes involved, even if they do sacrifice some of the allure of the unknown.
Ecological Rationality
Traditional definitions of rationality are concerned with maintaining internal order of beliefs and inferences, as we will see in the next section. But real organisms spend most of their time dealing with the external disorder of their environment, trying the make the decisions that will allow them to survive and reproduce (Tooby & Cosmides, 1998). To behave adaptively in the face of environmental challenges, organisms must be able to make inferences that are fast, frugal, and accurate. These real-world requirements lead to a new conception of what proper reasoning is: ecological rationality. Fast and frugal heuristics that are matched to particular environmental structures allow organisms to be ecologically rational. The study of ecological rationality thus involves analyzing the structure of environments, the structure of heuristics, and the match between them, as we will see throughout this book.
How is ecological rationality possible? That is, how can fast and frugal heuristics work as well as they do, and escape the tradeoffs between different real-world criteria including speed and accuracy? The main reason for their success is that they make a tradeoff on another dimension: that of generality versus specificity. While coherence criteria are very general—logical consistency for instance can be applied to any domain—the correspondence criteria that measure a heuristic’s performance against the real world require much more domain-specific solutions. What works to make quick and accurate inferences in one domain may well not work in another. Thus, different environments can have different specific fast and frugal heuristics that exploit their particular information structure to make adaptive decisions. But specificity can also be a danger: if a different heuristic were required for every slightly different decision-making environment, we would need an unworkable multitude of heuristics to reason with, and we would not be able to generalize to previously-unencountered environments. Fast and frugal heuristics avoid this trap by their very simplicity, which allows them to be robust in the face of environmental change and enables them to generalize well to new situations.
Exploiting environment structure. Fast and frugal heuristics can benefit from the way information is structured in environments. In Chapter 10, for instance, we will meet a fast and frugal heuristic for quantitative estimation that relies on the skewed distributions of many real-world variables such as city population size—an aspect of environment structure that traditional statistical estimation techniques would either ignore or even try to erase by normalizing the data. Standard statistical models, and standard theories of rationality, aim to be as general as possible, so they make as broad and as few assumptions as possible about the data to which they will be applied. But the way information is structured in real-world environments often does not follow convenient simplifying assumptions. For instance, whereas most statistical models are designed to operate on datasets where means and variances are independent, Karl Pearson (1897) noted that in natural situations these two measures tend to be correlated, and thus each can be used as a cue to infer the other (Einhorn & Hogarth, 1981, p. 66). While general statistical methods strive to ignore such factors that could limit their applicability, evolution would seize upon informative environmental dependencies like this one and exploit them with specific heuristics if they would give a decision-making organism an adaptive edge.
Robustness. How can simple domain-specific heuristics ever be about as accurate as complex general strategies that work with many free parameters? One answer lies in not being too specific. Simple heuristics are meant to apply to specific environments, but they do not contain enough detail to match any one environment precisely. General strategies that can be made to conform to a broad range of environments, on the other hand, can end up being too highly focused to be of much real use—having a large number of free parameters to fiddle with can be a hindrance. Imagine a compulsive Weather Channel watcher with too much time on his hands who decides to record the daily fluctuations in temperature and rainfall where he lives for a year. If he uses this exact daily data to determine his wardrobe choices the following year, wearing shorts this April 15 because it was hot and dry last April 15, he will often end up cold and wet. As accurate as his detailed weather model may be for describing the particular pattern for which it was constructed, its predictive value in other situations—other times or other locations—may be minimal. This failure of generalization, a phenomenon known as overfitting (e.g., Geman et al., 1992; Massaro, 1988b), stems from assuming that every detail is of utmost relevance. In contrast, if our weather-watcher had used many fewer parameters in his model, for instance just recording the average weekly temperature and rainfall and using that to infer how to dress accordingly a year later, he could have made much more accurate (weekly) predictions and ended up more comfortable, adapting to the general trends that occur year after year. As we will show in various chapters, models with many free parameters, from multiple linear regression to neural networks, can suffer from trying to be like the compulsive rain-spotter.
Thus, there is an important difference between the two typical applications of a strategy, fitting (modeling decisions for a given set of data) and generalization (predicting or inferring based on new data). In fitting, it is usually true that the more parameters a model has, and the more information (cues) it uses, the better it will fit given data. In generalization, in contrast, more is not necessarily better. A computationally simple strategy that uses only some of the available information can be more robust, making more accurate predictions for new data, than a computationally complex, information-guzzling strategy that overfits.
Robustness goes hand in hand with speed, accuracy, and especially information frugality. Fast and frugal heuristics can reduce overfitting by ignoring the noise inherent in many cues and looking instead for the “swamping forces” reflected in the most important cues. Thus, simply using only one or a few of the most useful cues can automatically yield robustness. Furthermore, important cues are likely to remain important. The informative relationships in the environment are likely to hold true when the environment changes – for instance, April is likely to be associated with showers in northern locations year after year. In contrast, the random fluctuations of noise and even the effects of smaller systematic factors may well frequently alter – for instance, May flowers may depend on many variable factors like temperature, rainfall, seed dispersal, and insect pests that collectively change more from one year to the next. Because of this pattern, fast and frugal heuristics that pay attention to systematic informative cues while overlooking more variable uninformative cues can ride out environmental change without suffering much decrement in performance. Laplace’s superintelligence would never overfit because it does not have to make uncertain predictions. But models of inference that try to be like a Laplacean superintelligence are doomed to overfitting, when they swallow more data than they can digest.
Studying ecological rationality enables us to go beyond the widespread fiction that basing decision making on more information and computation will always lead to more accurate inferences. This ideology dominates much research, leading to computational models of cognition that are based on information-hungry statistical methods (Gigerenzer & Murray, 1987), and more generally to evaluative judgments about what is good and bad cognition. For instance, many “dual process” theories in cognitive and social psychology characterize reasoning with dichotomies such as analytic versus heuristic, argumentative versus suggestive, rule-based versus associative, and mindful versus mindless (e.g., Evans, 1989; Sloman, 1996). The unquestioned assumption behind these theories is that the more laborious, computationally expensive, and non-heuristic the strategy, the better the judgments to which it gives rise. This more-is-better ideology ignores the ecological rationality of cognitive strategies. Consequently, it comes as a surprise to the dichotomy-makers when people perform better by violating one of these ideological dictums, for instance when people make better judgments by relying on their intuition than when they reason (Wilson & Schooler, 1991), or when someone’s forecasts of stock earnings decrease in accuracy as new information is added (Davis et al., 1994; see also Ambady & Rosenthal, 1992). There is a point where too much information and too much information processing can hurt. Cognition is the art of focusing on the relevant and deliberately ignoring the rest. We take the same approach to modeling cognition.
Performance in Real-World Environments
As mentioned earlier, bounded rationality is often characterized as a view that takes into account the cognitive limitations of thinking humans—an incomplete and potentially misleading characterization. If we want to understand how real human minds work, we must look not only at how our reasoning is “limited” compared to that of supernatural beings, but also at how our minds are adapted to real-world environments. This two-sided conception of bounded rationality should inform our choice of criteria by which to evaluate the performance of heuristics.
One set of criteria that is often used to evaluate judgments and decisions is the laws of logic and probability theory. For instance, if judgments are consistent (e.g., I always think that event A is more likely than B) and transitive (I think A is more likely than B, B is more likely than C, and therefore that A is more likely than C), this is taken as an indication that the underlying decision strategies are rational. If such criteria are violated, this is typically held to be a sign of irrationality on the part of the decision maker. These laws of logic and probability are called coherence criteria because they are primarily concerned with the internal logical coherence of judgments rather than with how well they help us to make useful decisions in the real world. If you believe there is a probability of 90% that Elvis is still alive and a probability of 10% that he is not, your beliefs are at least coherent, in that you give the two opposite possibilities together a 100% chance, as probability theory says you must. But if they lead you to spend long hours in cornfields waiting for his UFO to land, these beliefs are not doing you much real-world good. Instead of considering these issues of content and real-world adaptiveness, most experimental research programs aimed at demonstrating the rationality or (usually) irrationality of humans and animals have used the abstract coherence criteria. For instance, many claims that there are systematic irrational fallacies in human reasoning are based entirely on a violation of some rule or other of logic or probability (e.g., Tversky & Kahneman, 1983; Wason, 1983). Similarly, it has been claimed that “Monkeys are rational!” (McGonigle & Chalmers, 1992) following the observation that squirrel monkeys make choices that conform to transitivity.
This book adopts a different, adaptive view of rational behavior. We do not compare human judgment with the laws of logic or probability, but rather examine how it fares in real-world environments. The function of heuristics is not to be coherent. Rather, their function is to make reasonable, adaptive inferences about the real social and physical world given limited time and knowledge. Hence, we should evaluate the performance of heuristics by criteria that reflect this function. Measures that relate decision-making strategies to the external world rather than to internal consistence, such as accuracy, frugality, and speed, are called correspondence criteria (Hammond, 1996). As Egon Brunswik (1964) observed, the mind and the environment are like a husband and wife couple who must come to terms with one another by mutual adaptation. However, owing to the focus on coherence in much research on reasoning and decision making, the couple has become estranged. Our aim is to get this couple corresponding again, even if they cannot be coherent.
Indeed, the two kinds of criteria, coherence and correspondence, can sometimes be at odds with each other. For instance, in social situations, including some competitive games and predator-prey interactions, it can be advantageous to exhibit inconsistent behavior in order to maximize adaptive unpredictability and avoid capture or loss (Driver & Humphries, 1988). In Chapters 4 and 5, we will meet a similarly illogical heuristic—the Minimalist heuristic—that violates transitivity but nevertheless makes fairly robust and accurate inferences in particular environments. Thus, intransitivity does not necessarily imply high levels of inaccuracy, nor does transitivity guarantee high levels of accuracy—logic and adaptive behavior are logically distinct.
To conclude: Heuristics are not simply hobbled versions of optimal strategies. There are no optimal strategies in many real-world environments in the first place. This does not mean, though, that there are no performance criteria in the real world. As a measure of the success of a heuristic, we compare its performance with the actual requirements of its environment, which can include making accurate decisions, in a minimal amount of time, and using a minimal amount of information. We have thus replaced the multiple coherence criteria stemming from the laws of logic and probability with multiple correspondence criteria relating to real-world decision performance. But there is a further difference between these two sets of multiple criteria: While all coherence criteria must be met for a decision method to be deemed rational, correspondence criteria can be considered in relation to each other. In some environments, for instance, it may be more important to make a decision quickly rather than focusing on accuracy. However, one of the surprising empirical results reported in this book is that simple heuristics need not always make such tradeoffs. We will show that, when compared to some standard benchmark strategies, fast and frugal heuristics can be faster, more frugal, and more accurate at the same time. No tradeoff need be considered.
Do People Use Fast and Frugal Heuristics?
The research program described so far encompasses three big questions: (1) What are reasonable heuristic principles for guiding information or alternative search, stopping search, and making a decision using the results of that search? (2) When and why do these heuristics perform well, that is, how can they be ecologically rational? (3) How well do fast and frugal heuristics actually perform in real-world environments? Exploring these three questions is sufficient if we are interested in investigating new heuristics for various applied settings—the realms of artificial intelligence and decision-support systems, for instance. But if we are also concerned to discover the principles that guide natural human and animal behavior, we must add a fourth question to our research program: What is the evidence that humans or animals use specific fast and frugal heuristics?
We know rather little about the heuristic principles of limited search and stopping that people and animals use. One major reason for this is that the typical experimental task eliminates search in the first place (but see e.g., Connolly & Gilani, 1982; Payne et al., 1993; Saad & Russo, 1996). Researchers usually sidestep questions of search by using tasks in which all pieces of information—usually only two or three—are already conveniently laid out in front of the participant. We refer to this type of task as inference from givens, as opposed to inference from memory or inference from the external environment, both of which require search (Gigerenzer & Goldstein, 1996a). For instance, the majority of psychological studies of categorization use artificial objects (e.g., drawings of faces or fishes) that vary on only a few cues. To classify a new object, the participant is not supposed to perform a search for cues in her memory or in the environment, but rather is expected merely to use the few immediately available cues presented in the stimuli (see Chapter 11 for a discussion of this problem and a fast and frugal categorization heuristic designed to tackle more realistic multiple-cue situations). Theories of cognition and the experimental tasks used to test those theories often conspire hand in hand to overlook limited search and stopping rules. But experiments in which search is obviated are unsuitable for testing models of ecological and bounded rationality that rely on limited information search as a central component.
Ironically, one reason why so little attention has been devoted to heuristic principles of limited search may stem from the use of a fast and frugal heuristic itself. The tools-to-theories heuristic of scientific discovery (Gigerenzer, 1991a) predicts that the laboratory tools entrenched in the daily routine of cognitive scientists will tend to be adopted as models of mind. In the 1950s and 60s, statistical methods of inference were institutionalized in experimental psychology, based on a mishmash of Fisher’s null hypothesis testing and Neyman and Pearson’s decision theory. None of these institutionalized tools dealt with search and stopping rules, in contrast to other well-known statistical tools that do (e.g., the sequential analysis of Wald, 1947). In accordance with the tools-to-theories heuristic, many researchers have since proposed theories that model cognitive processes after these institutionalized statistical tools, and that therefore also ignore the necessity of modeling search and stopping rules. For example, in his causal attribution theory, Kelley (1967) proposed that the mind attributes effects to causes in the same way that cognitive researchers generally do, that is, by calculating Fisher’s analysis of variance. As another instance, in what became known as signal detection theory, Tanner and Swets (1954) suggested that the mind discriminates between two stimuli like a statistician of the Neyman-Pearson school would test between two statistical hypotheses. As mentioned above, these statistical approaches of Fisher and Neyman-Pearson did not include the concept of search, and so, following the tools-to-theories explanation, this is why neither the cognitive theories stemming from these statistical tools nor the experimental tasks designed to test them consider search processes, a legacy we are left with today (Gigerenzer & Goldstein, 1996b; Gigerenzer & Murray, 1987).
In contrast to the lack of work on heuristic principles for guiding and stopping search, decision rules have been the focus of a great deal of research and theorizing. For instance, psychologists have asked whether children integrate information additively, multiplicatively, or in some other way (e.g., Gigerenzer & Richter, 1990), and whether adults integrate information by Bayes’s rule or by averaging (e.g., Birnbaum & Mellers, 1983). But again these questions are typically investigated with experimental designs where information is restricted to only two or three cues presented to participants, removing the need for any search. As a consequence, the results of these studies may not tell us much about the heuristic decision principles used in more realistic situations where information or alternatives must be actively sought.
Summary of Our View of Rationality
The research program just described is designed to elucidate three distinct but interconnected aspects of rationality (see also Chase, Hertwig, & Gigerenzer, 1998):
1. Bounded rationality. Decision-making agents in the real world must arrive at their inferences using realistic amounts of time, information, and computational resources. We look for inference mechanisms exhibiting bounded rationality by designing and testing computational models of fast and frugal heuristics and their psychological building blocks. The building blocks include heuristic principles for guiding search for information or alternatives, stopping the search, and making decisions.
2. Ecological rationality. Decision-making mechanisms can exploit the structure of information in the environment to arrive at more adaptively useful outcomes. To understand how different heuristics can be ecologically rational, we characterize the ways information can be structured in different decision environments and how heuristics can tap that structure to be fast, frugal, accurate, and otherwise adaptive at the same time.
3. Social rationality. The most important aspects of an agent’s environment are often created by the other agents it interacts with. Thus, predators must make crucial inferences about the behavior of their prey (see Chapter 12), males and females must make decisions about others they are interested in mating with (Chapter 13), and parents must figure out how to help their children (Chapter 14). Social rationality is a special form of ecological rationality, and to study it we design and test computational models of fast and frugal heuristics that exploit the information structure of the social environment to enable adaptive interactions with other agents. These heuristics can include socially adaptive building blocks, such as emotions of anger and parental love and social norms, which can act as further heuristic principles for search, stopping, and decision (we return to this point below).
These three aspects of rationality look toward the same central goal: to understand human behavior and cognition as it is adapted to specific environments (ecological and social), and to discover the heuristics that guide adaptive behavior.
How Our Research Program Relates to
Earlier Notions of Heuristics
The term “heuristic” is of Greek origin, meaning “serving to find out or discover.” From its introduction into English in the early 1800s up until about 1970, “heuristic” referred to useful, even indispensable cognitive processes for solving problems that cannot be handled by logic and probability theory (e.g., Polya, 1954; Groner at al., 1983). After 1970, a second meaning emerged in the fields of psychology and decision making research: fallacious and to-be-avoided cognitive processes that people often use in situations where logic and probability theory should be applied instead (e.g., Tversky & Kahneman, 1974). We now explore the 20th century changes in the concept of heuristic in a bit more detail, and show how our own use of the terms fits into the historical context.
In 1905, the 26-year-old Albert Einstein published his
first fundamental paper in quantum physics, entitled “On a heuristic point of
view concerning the generation and transformation of light.” In that Nobel
prize-winning paper, Einstein used the term “heuristic” to indicate that he
considered the view he presented therein as incomplete, false even, but still
useful. Einstein could not wholeheartedly accept the quantum view of light that
he started to develop in this paper, but he believed that it was of great
transitory use on the way to building a more correct theory (Holton, 1973, p.
360-361). As used by Einstein, then, a heuristic is an approach to a problem
that is necessarily incomplete given the knowledge available, and hence
unavoidably false, but which is useful nonetheless for guiding thinking in
appropriate directions (see also Wimsatt, 1987).
At few decades later, Max Wertheimer (a close friend of Einstein’s), Karl Duncker, and other Gestalt psychologists spoke of heuristic reasoning, but with a slightly different meaning from Einstein’s. Gestalt psychologists conceptualized thinking as an interaction between inner mental processes and external problem structure. On this view, heuristic methods such as “looking around” and “inspecting the problem” are first used to guide the search for appropriate information in the environment, which is then restructured or reformulated by inner processes (e.g., Duncker, 1935/45). It is in this tradition that Herbert Simon and Allen Newell modeled heuristics for search, replacing the somewhat vague methods of the Gestalt school with much more precise computational models. With the advent of information processing theory in cognitive psychology, a heuristic came to mean a useful shortcut, an approximation, or a rule of thumb for guiding search, such as a strategy that a chess master uses to reduce the enormous space of possible moves at each point in a game.
We use the term “heuristic” in the same positive sense as these earlier theorists, emphasizing its beneficial role in guiding search, and following Simon and Newell’s emphasis on creating precise computational models. However, we break with the past tradition of using well-defined artificial settings for the study of heuristics, such as mathematical problems (Polya, 1954) or the games of chess and cryptoarithmetic that Newell and Simon (1972) investigated. Instead, our research addresses how fast and frugal heuristics can make inferences about unknown aspects of real-world environments.
The research most closely related to the ABC program on fast and frugal heuristics is that on adaptive decision making and on simple classification rules in machine learning. In their work on the “adaptive decision maker”, Payne, Bettman, and Johnson (1993) studied the trade-off between accuracy and effort for various choice strategies, including lexicographic rules and Elimination by Aspects (Tversky, 1972). Payne and colleagues emphasized that a decision maker has a multitude of strategies available and chooses between them depending on their costs and accuracy given constraints such as time pressure. This important work has many connections with our own program, as we will see throughout this book, but there are also important differences that will become evident. One such distinction is that Payne and colleagues focused on preferences, such as between hypothetical job candidates or randomly generated gambles, rather than on inferences about the real world, such as which soccer team will win or which of two cities is larger. This is why they could not measure the accuracy of strategies in terms of their ability to predict real-world outcomes. Instead, they measured accuracy by how closely a strategy could match the predictions of a weighted additive rule, which is the traditional gold standard for rational preferences. As a consequence, in Payne, Bettman, and Johnson’s research a heuristic can never be better than a weighted additive rule in accuracy (though it may require less computational effort). In contrast, by measuring the performance of all competing strategies against external real-world criteria, we find that fast and frugal heuristics can be more accurate than a weighted additive rule both in theory (Chapter 4) and in practice (Chapter 5). Research in machine learning similarly focuses on inferences about real-world environments, again allowing accuracy to be measured objectively. Work on simple classification rules that use only one or a few cues (e.g., Holte, 1993; Rivest, 1987) has demonstrated that fast and frugal methods can be accurate, as well as being robust generalizers owing to their limited parameter use.
A very different notion emerged in psychology in the early 1970s, emphasizing how the use of heuristics can lead to systematic errors and lapses of reasoning that indicate human irrationality. This “heuristics-and-biases” program launched by Tversky and Kahneman (1974) tainted the idea of simple mental mechanisms by attaching them to the value-laden “bias” term in a single inseparable phrase. Within this program, heuristics were invoked as the explanation (or scapegoat) whenever errors—mainly deviations from the laws of probability—were found in human reasoning. Although Tversky and Kahneman (1974) repeatedly asserted that heuristics sometimes succeed and sometimes fail, they interpreted all of their experimental results as indicating some kind of fallacy, which they attributed (usually post hoc) to one of three main heuristics: representativeness (judgments influenced by what is typical), availability (judgments based on what come easily to mind), or anchoring and adjustment (judgments relying on what comes first).
The heuristics-and-biases program suggests that ordinary people are cognitive misers who use little information and little cognition and thus are largely unable to estimate probabilities and risks. Some have taken this to mean that it might be best to cut the general public out of making important social and political decisions, such as those concerning the regulation of the nuclear industry and other potentially hazardous new technologies. In the words of a Newsweek article reporting on heuristics-and-biases research: “Most people ... are woefully muddled information processors who often stumble along ill-chosen short-cuts to reach bad conclusions”(1987, p. 24). However, Tversky and Kahneman also argued that leaving decisions to experts may not be an improvement, as they can be subject to similar mistakes. Given this pessimistic view, it is hard to know where to turn for reasonable decisions.
The narrowly-defined “fallacies” touted by the heuristics-and-biases program have not only been deemed irrational, but they have also been interpreted as signs of the bounded rationality of humans (e.g., Thaler, 1991, p. 4). Equating bounded rationality with irrationality in this way is as serious a confusion as equating it with constrained optimization. Bounded rationality is neither limited optimality nor irrationality.
Our research program of studying fast and frugal heuristics shares some basic features with the heuristics-and-biases program. Both emphasize the important role that simple psychological heuristics play in human thought, and both are concerned with finding the situations in which these heuristics are employed. But these similarities mask a profound basic difference of opinion on the underlying nature of rationality, leading to very divergent research agendas: In our program, we see heuristics as the way the human mind can take advantage of the structure of information in the environment to arrive at reasonable decisions, and so we focus on the ways and settings in which simple heuristics lead to accurate and useful inferences. In contrast, the heuristics-and-biases approach views heuristics as crutches that the limited human mind is forced to rely upon despite their inferior decision-making ability, and hence researchers in this tradition seek out cases where heuristics can be blamed for poor reasoning. We discuss two further distinctions here that follow from this basic difference; for a more detailed analysis, see Gigerenzer (1991b, 1994, 1997; Gigerenzer & Murray, 1987), and for arguments in favor of each side, see the debate between Kahneman and Tversky (1996) and Gigerenzer (1996).
The first distinction is that the ABC program opts for computational models of heuristics instead of vague labels. After three decades of research, the heuristics-and-biases program has generated only nebulous, if plausible, proposals for simple mechanisms of (poor) reasoning, primarily the three heuristics mentioned earlier, representativeness, availability, and anchoring-and-adjustment. These one-word labels at once explain too little and too much: too little, because the underlying processes are left unspecified, and too much, because, with sufficient imagination, one of them can be fit to almost any empirical result post hoc. For instance, “base-rate neglect,” or ignoring the frequency with which different alternatives occur in the environment when making decisions about them, is commonly attributed to the representativeness heuristic. However, the opposite result, overweighting of base rates (or “conservatism,” Edwards, 1968), is as easily “explained” by anchoring (on the base rate) and adjustment (Gigerenzer & Murray, 1987). There are two ways a theory can fail, by being wrong, or by being not even wrong, but merely indeterminate and imprecise. The heuristics-and-biases program has too often fallen into the latter category. But we would rather risk the former fate, because indeterminate theories hinder scientific progress by resisting attempts to prove, disprove, or improve them. In this book, we therefore propose computational models of heuristics, putting our theoretical cards on the table so that others can see them—and even pick them up and play with them.
The second distinction is a normative one. The ABC program dispenses with the focus on coherence criteria (e.g., the laws of probability) as the yardsticks of rationality. Instead, we study the correspondence-based performance of heuristics in real-world environments, situations where optimal coherent strategies are often not known or not feasible. In contrast, proponents of the heuristics-and-biases program typically assume that each reasoning task has exactly one normative answer, which is derived by applying a law of probability in a content-blind way, without looking at the specifics of the task or environment. Our view liberates fast and frugal heuristics from their role in the heuristics-and-biases program as the harbingers of coherence-defined irrationality and holds them up as tools for adaptive and accurate decision-making in real environments.
To summarize the place of our research in its
historical context, the ABC program takes up the traditional notion of
heuristics as an essential cognitive tool for making reasonable decisions. We
specify the function and role of fast and frugal heuristics more precisely than
has been done in the past, by building computational models with specific
principles of information search, stopping, and decision making. We replace the
narrow, content-blind norms of coherence criteria with the analysis of
heuristic accuracy, speed, and frugality in real-world environments as part of
our study of ecological rationality. Finally, whereas the heuristics-and-biases
program portrays heuristics as a hindrance to sound reasoning, rendering Homo
sapiens not so sapient, we see fast and frugal heuristics as enabling us to
make reasonable decisions and behave adaptively in our environment—Homo
sapiens would be lost without them.
The Adaptive Toolbox
Gottfried Wilhelm Leibniz had a beautiful dream. He dreamed of a universal logical language, the Universal Characteristic, that would replace all reasoning (Leibniz, 1677/1951). The Universal Characteristic had two parts: (1) an alphabet of human thought, that is, a system of primitive characters that stand for irreducible simple concepts and form an inventory of real things, and (2) a calculus of reasoning that combines the elements of this alphabet. While Robert Boyle had searched for the alphabetic elements of chemistry, Leibniz aimed for an even more ambitious target: understanding the universal language in which God had written the book of nature. He saw such knowledge of God’s creation as the most important goal anyone could strive for. Leibniz believed that the Universal Characteristic would put an end to scholarly bickering and clamorous controversy—people could stop shouting at one another and settle matters peacefully by sitting down with pencil and paper and saying “Let’s calculate.” All matters of science and morality would be solved, and we would live in the best of all possible worlds. Young Leibniz made the optimistic prediction about the Universal Characteristic’s development period that “a few selected persons might be able to do the whole thing in five years” (Leibniz, 1677/1951). (Similar sentiments have been uttered over the years concerning psychology and artificial intelligence.) For some time, many Enlightenment thinkers believed that the mathematical theory of probability could make Leibniz’s dream a reality. But by the 1840s, mathematicians had given up the task of reducing rational reasoning to a general calculus as thankless and even antimathematical (Daston, 1988). However, as we saw earlier in our discussions of demons, there are still many theorists in a variety of fields to this day who have not given up the logic of this dream.
The multitude of simple concepts comprising Leibniz’s alphabet of human thought were all to be operated on by a single general-purpose tool such as probability theory. But no such universal tool of inference could be found. Just as a mechanic will pull out specific wrenches, pliers, and spark-plug gap gauges for each task in maintaining a car’s engine rather than merely hitting everything with a large hammer, different domains of thought require different specialized tools. This is the basic idea of the adaptive toolbox: the collection of specialized cognitive mechanisms that evolution has built into the human mind for specific domains of inference and reasoning, including fast and frugal heuristics (see also Bettman, 1979; Cosmides & Tooby, 1992; Payne et al., 1993). The notion of a toolbox jumbled full of unique one-function devices lacks the beauty of Leibniz’s dream of a single all-purpose inferential powertool. Instead, it invokes the more modest but surprising abilities of a “backwoods mechanic and used parts dealer” (as Wimsatt, in press, describes Nature) who can provide serviceable solutions to most any problem with just the things at hand.
The adaptive toolbox contains psychological (as opposed to morphological or physiological) adaptations (Tooby & Cosmides, 1992). These include so-called “lower-order” perceptual and memory processes which can be fairly automatic, such as depth perception, auditory scene analysis, and face recognition, as well as “higher-order” processes that are based on the “lower” processes and can be at least partly accessible to consciousness. Higher-order mental processes include the examples we have discussed earlier of inferring whether a heart attack victim should be treated as a high- or low-risk patient and deciding whether or not to marry. The focus of this book is on fast and frugal heuristics for higher-order cognitive processes that call upon lower-order processes of cue perception and memory.
Lower-order perceptual and memory processes such as
face and voice recognition are complex and difficult to unravel, in part
because they make use of massively parallel computations. No one has yet
managed to build a machine that recognizes faces as well as a two-year-old
child. Now consider a higher-order decision mechanism that makes inferences
based on these processes, the recognition heuristic introduced in Chapter 2.
This fast and frugal heuristic uses recognition to make rapid inferences about
unknown aspects of the world: For instance, food whose taste one recognizes is
probably safer than unrecognized food, and a university whose name one has
heard of probably provides a more prestigious education than one whose name is
unfamiliar. Although the mechanisms of recognition memory may be intricate and
complex, the recognition heuristic can be described as an algorithm just a few
steps long. We do not need to know precisely how recognition memory works to
describe a heuristic that relies on recognition. This example illustrates an
apparently paradoxical thesis: Higher-order cognitive mechanisms can often
be modeled by simpler algorithms than can lower-order mechanisms.
This thesis is not new. It has been proposed in various forms over the past century, as for example by proponents of the Würzburg school of psychology in the early 20th century (Kusch, in press) and more recently by Shepard (1967). The thesis has limits as well, of course: Some higher-order processes, such as the creative process involved in Darwin’s development of the theory of natural selection, are probably beyond the grasp of fast and frugal heuristics. But we believe that simple heuristics can be used singly and in combination to account for a great variety of higher-order mental processes that may at first glance seem to require more complex explanation, as we will show throughout this book.
Emotions, Social Norms, and Imitation
Although we focus on cognitive heuristics in this book, it is important to point out that emotions can also function as heuristic principles for guiding and stopping information search. For instance, falling in love can be seen as a powerful stopping rule that ends the current search for a partner (at least temporarily) and strengthens commitment to the loved one. Similarly, feelings of parental love, triggered by one’s infant’s presence or smile, can be described as a means of preventing cost-benefit computations with respect to proximal goals, so that the question of whether or not it is worthwhile to endure all the sleepless nights and other challenges associated with baby care simply never arises. Emotions are good examples of building blocks in the adaptive toolbox that are substantially domain-specific rather than domain-general (Tooby & Cosmides, 1990): For instance, while parental love is designed to help parents to solve the adaptive task of protecting and providing for their offspring, disgust functions to address the adaptive challenge of avoiding being sickened by spoiled food. There is no general-purpose all-encompassing emotion.
Social norms and social imitation can also help us make decisions with limited time and knowledge. Following heuristics such as “eat what older and experienced conspecifics eat” or “prefer mates picked by others” can speed up decision making by reducing the need for direct experience and information-gathering. These forms of social rationality can be found throughout the animal world: For instance, female guppies have a tendency to copy the mate choices of other female guppies that is powerful enough to reverse their prior preferences for one male over another (Dugatkin, 1996), and female quail use a related form of mate copying (Galef & White, 1998). In humans, in addition to individual and media-fueled mate copying, academic hiring often seems to follow a similar heuristic.
Thus the adaptive toolbox contains decision-making heuristics that employ emotions, norms, and imitation in addition to the cognitive building blocks outlined earlier. These additional heuristic principles are particularly important in the realm of social rationality.
How Are Heuristics Selected?
How does the mind choose which heuristic
in the adaptive toolbox to apply to a specific problem? There may mot be as
much choice as it initially seems. The most important reason for this is that
specific tasks call for specific tools—that is, each heuristic is specialized
for certain classes of problems, which means that most of them are not
applicable in a given situation. There are two (overlapping) forms of domain
specificity used throughout this book that can determine heuristic choice:
specific adaptive tasks, such as mate choice or parental investment; and
specific inference tasks, such as categorization or estimation. Clearly, a
heuristic designed to make a choice between two alternatives will not be
suitable for categorization, nor will a mate choice heuristic help in judging
habitat quality. The domain-specific bins in the adaptive toolbox will often
hold only a single appropriate tool.
In those cases where there is more than one applicable heuristic, the knowledge that the decision maker has can be used to select the heuristic. For instance, if a person knows that certain cues can be used to decide between two options, but not which cues are better indicators than others, she does not have enough information (about how to order the cues) to apply a fast and frugal heuristic we call Take The Best (Chapter 4). However, she can use the even simpler Take The Last choice heuristic, which only needs to know what cues to use, and not what order to use them in. If she does not even know any cues to use, but at least recognizes one option and not the other, she can still apply the simplest fast and frugal heuristic: the recognition heuristic (Chapter 2). In this way, the level of knowledge can make further selections among domain-specific heuristics in the adaptive toolbox.
Other external factors, such as time pressure and success, may further help to select heuristics (Johnson & Payne, 1985). There are also certain situations where it is adaptive to alternate between multiple strategies, either randomly, yielding unpredictable protean behavior that can be useful when engaging competitors or fleeing from predators (Driver & Humphries, 1988), or systematically, yielding individual differences in decisions that help avoid conflicts such as everyone crowding into the local bar on the same night each week (Arthur, 1994). We assume that all of the factors involved in selecting decision-making mechanisms from the adaptive toolbox will themselves be used in a fast and frugal manner to make the tool choice, rather than being handed over to a hidden computationally elaborate demon who undermines the spirit of fast and frugal cognition by optimizing heuristic choice.
The tools in the adaptive toolbox are made from more primitive components, including the heuristic principles of information search, stopping, and decision discussed earlier. New tools can also be fashioned from old tools, much as a handle added to a chopping stone creates an axe. Thus for instance the Take the Best heuristic presented in Chapter 4 is made from the more primitive (and probably earlier evolved) recognition heuristic of Chapter 2 along with additional heuristic principles. This constructive view applied to the mental tools themselves distinguishes the adaptive toolbox image from the similar metaphor of the mind as a Swiss Army Knife (Cosmides & Tooby, 1992). Both analogies emphasize that the mind uses a collection of many specifically designed adaptive strategies rather than a few general-purpose powertools, but the toolbox metaphor puts more emphasis on the possibility of recombining tools and building blocks and the nesting of heuristics.
Beyond Demons and Nightmares
In the world of academic thought, there are powerful
demons that few people would want to tangle with, such as irrationality and
mysticism. But there are also demons that some researchers seem to love,
inviting them into mental theories at every opportunity—unbounded rationality
and optimization under constraints sitting at the top of the demonic hierarchy.
These popular demons embody characteristics that are unquestionably desirable,
such as being able to calculate the future, but nonetheless absolutely
unattainable for mortal humans. Why have so many social scientists idealized
our human knowledge and abilities in ways aspiring to the characteristics of
some Supreme Being, rather than reflecting our more real limitations? Is it an
intellectual holdover from the pre-Darwinian view of mankind as distinct from
the rest of Nature?
The fascination with what is optimal in thought and behavior does reflect a certain sense of beauty and morality. Leibniz’ dream of a universal calculus exhibits the aesthetics and the moral virtue of this ideal, as does Laplace’s omniscient superintelligence. Cognitive scientists, economists, and biologists have often chased after the same beautiful dreams by building elaborate models endowing organisms with unlimited abilities to know, memorize, and compute. These heavenly dreams, however, tend to evaporate when they encounter the physical and psychological realities of the waking world. Mere mortal humans cannot hope to live up to these dreams, and instead appear irrational and dysfunctional when measured against their fantastic standards. On earth, heavenly dreams become nightmares.
In the face of this nightmarish dilemma, many researchers have still preferred to keep dreaming that humans can approximate these exacting standards, rather than surrender to an ungodly picture of human irrationality and stupidity. The choice, however, is not between an unrealistic dreaming rationality and a realistic nightmare irrationality. There is a third vision that dispenses with this opposition: rationality through simplicity, and accuracy through frugality.
This book is the story of our successes and remaining challenges in understanding how minds can be fast, frugal, and accurate at the same time, making adaptive inferences about an unknown world through uncertain cues. It is also the story of an interdisciplinary group who set out to journey together from the land of demons to the land of ecologically rational beings, learning the use of multiple methods of inquiry and the value of multiple points of view from each other. When we began our travels almost three years ago, we never imagined how fascinating the voyage would be, nor the many new things our eyes would see.
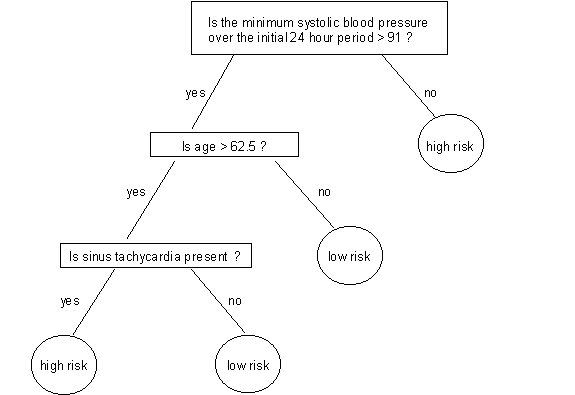
Figure 1-1: A simple decision tree for classifying incoming heart attack patients into high risk and low risk patients (adapted from Breiman et al., 1993).
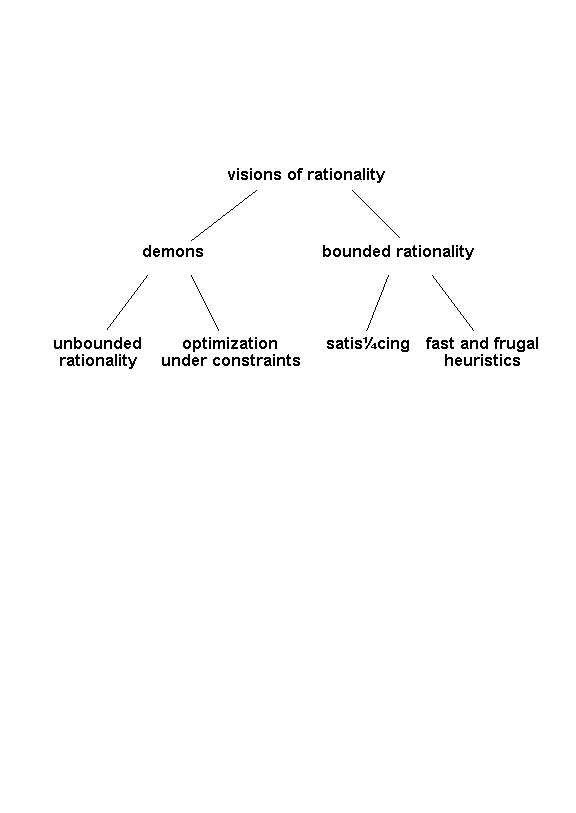
Figure 1-2: Visions of rationality