A partir destes factos concebeu-se uma metodologia de mapeamento genético, que baseada nas estimativas de frequências de gâmetas recombinantes vai fazendo alinhar os loci em cada grupo de ligação. Uma experiência típica de mapeamento envolve três loci ligados para a medição de duas taxas de recombinação, e o testcross aos tri-híbridos da F1, havendo dois passos na análise dos resultados na F2: i) determinar qual a ordem dos loci (por exemplo, X——Y——Z) e ii) medir as duas distâncias intercalares (de X para Y e de Y para Z).
Exemplo
P | FFggHH | × | ffGGhh | |||||
G | FgH | fGh | ||||||
F1 | (haplótipos) | FgH / fGh | × | ffgghh | ||||
F2 (fenótipos esperados) | FgH fGh | FGH fgh | FGh fgH | Fgh fGH | ||||
Repare-se que cada coluna da F2 representa duas populações de gâmetas da F1 que são produtos complementares do mesmo tipo de meiose, e pela 1ª lei de Mendel as suas frequências esperam-se iguais entre si. A primeira coluna corresponde aos haplótipos da F1, e conterá por isso o par mais frequente. Em contrapartida, o par menos frequnte será aquele que resulta da dupla recombinação, isto é, de um crossover em cada um dos dois segmentos em estudo. Introduzindo frequências hipotéticas na F2:
| F2 (N=1200) | FgH 520 | FGH 9 | FGh 0 | Fgh 81 |
| fGh 502 | fgh 12 | fgH 0 | fGH 76 |
Há um par que não aparece, presumivelmente porque a dimensão da amostra não era suficiente para revelar os eventos de recombinação dupla, mas isso só se comprova aumentando-a numa repetição desta experiência (por exemplo para 12000 indivíduos na F2). Entretanto, vai partir-se dessa hipótese (o par ausente seriam os duplos recombinantes) para identificar a ordem dos loci: o que há de comum entre os haplótipos parentais e os supostos duplos recombinantes é o arranjo em repulsão gH / Gh, indicativo que são estes dois loci que se encontram nas extremidades do segmento cromossómico em estudo, donde
G ———— F ———— H
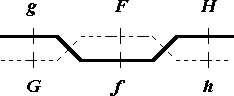
Cada classe dupla-recombinante resulta de haver um crossover num dos segmentos e outro crossover no outro segmento, restabelecendo os haplótipos da F1 para as extremidades, com o rearranjo dos genes centrais:
Tendo assim determinado o arranjo dos loci, há apenas que efectuar o cálculo das duas distâncias, G——F e F——H:
| rGF = (9 + 12 + 0 + 0) / 1200 = 1, 75% | rFH = (81 + 76 + 0 + 0) / 1200 ≈ 13,08% |
Os duplos recombinantes, se os houvesse, entrariam em ambos os cálculos. O mapa fica assim:
| 1,75 | 13,08 | |||
| G | — | F | ———————— | H |
A unidade de mapa é o centimorgan (cM), correspondendo 1 cM a 1% de taxa de recombinação.
Tendo estes dados, talvez seja de admirar que não houvesse duplos recombinantes, pois no conjunto das duas classes esperar-se-iam NrGFrFH ≈ 2,75 indivíduos. Embora se possam invocar os acasos da amostragem (a distribuição de Poisson prevê a probabilidade de e–2,75 ≈ 0,064 para 0 ocorrências), sabe-se que em regra os duplos recombinantes ocorrem abaixo da expectativa devido a um fenómeno de interferência que pode ser entendido da seguinte forma: se houver um crossover num dos segmentos, por exemplo no F — H, então torna-se "menos provável" que haja, na mesma célula, também um crossover no outro segmento ( G — F).
O número de duplos recombinantes que de facto ocorrem é assim função da dimensão da amostra e das taxas de recombinação, mas também de um coeficiente de coincidência (c.c.) característico para o segmento compreendendo os três loci. O valor de c.c. obtém-se do quociente entre os recombinantes duplos observados e os esperados:
O aparente valor de 100% para a interferência nesta experiência é, em rigor, maior do que 63,6%, visto que só é possível afirmar que ccGH < 1/2,75. Ainda neste exemplo, se os resultados fossem:
| F2 (N=12000) | FgH 5083 | FGH 101 | FGh 1 | Fgh 799 |
| fGh 5101 | fgh 96 | fgH 4 | fGH 815 |
então rGF = 1,68%, rFH = 13,49%, NrGFrFH = 27,25, e o coeficiente de coincidência ccGH = 5/27,25 = 0,1835.
Portanto, a interferência neste segmento seria aproximadamente 82,65%. Qualquer experiência subsequente contaria assim com N×0,1835rGFrFH duplos recombinantes (em princípio, quaisquer que fossem as combinações haplotípicas na F1). Na F2 anterior, com 1200 indivíduos apenas, esta expectativa seria de 0,5040, pelo que a ausência de duplos recombinantes era afinal muito provável.
|
Não parece haver ainda uma demonstração experimental dos mecanismos moleculares da interferência, embora se aceite o conceito que a tensão mecânica resultante de cada crossover inibe a ocorrência de outro crossover na sua vizinhança. |
Há uma importante consequência prática da interferência: o mapeamento é tanto mais preciso quanto mais próximos entre si se encontrem os loci (por exemplo no espaço de 5 cM ou até menos), pois devido à interferência é quase impossível que haja recombinações que passem despercebidas: por exemplo, da mesma maneira que era em teoria possível haver recombinantes duplos no segmento G—H, detectáveis pelas classes FGh e fgH, não seria muito diferente a probabilidade de haver nas classes parentais indivíduos que seriam na verdade duplos recombinantes só no segmento F—H.
Esta metodologia aplica-se a todos os loci que se expressam na fase diplóide e foi desenvolvida a partir de 1913, com a Drosophila melanogaster, pelo grupo norte-americano de Morgan, Sturtevant, Bridges e outros. Embora em cada experiência de mapeamento se meçam distâncias, ou seja, posições relativas, nos mapas que resumem toda a informação acumulada para cada grupo de ligação definem-se posições em relação a um ponto para o qual se convenciona atribuir a posição 0, ponto esse que é marcado por um locus que se deduz encontrar-se num dos extremos do cromossoma. Por acumulação de distâncias, é frequente certos grupos de ligação abrangerem mais de 50 e até 100 cM, apesar da taxa de recombinação entre cada par de genes não poder em caso algum ir além dos 50%. Por outras palavras, a exactidão do método degrada-se fortemente para além de certa distância, por causa dos crossovers duplos, quádruplos, etc., e o ideal é medir distâncias relativamente curtas (o suficiente para que a interferência seja próxima de 100%).
No caso de organismos que produzem pouca descendência o método é válido em teoria, mas apenas entre loci bastante afastados, existido certos algoritmos que permitem estimar o número de crossovers em múltiplo de 2 para obter distâncias acima de 50 cM.
A localização citogenética de certos loci foi conseguida inicialmente em associação com anomalias estruturais, e mais recentemente com o auxílio de sondas moleculares. Como se esperava, corresponde à ordem prevista pelos mapas de ligação, mas em regra há uma grande discrepância entre as distâncias medidas por taxas de recombinação e as distâncias observadas directamente. Daí que, contrapondo-se os mapas de ligação aos mapas físicos, haja uma tendência mais ou menos uniforme para taxas de recombinação relativamente mais baixas nas proximidades dos centrómeros, sendo o inverso nas regiões sub-teloméricas (ver figura 8); este resultado indica que a interferência está longe de ser uniforme na extensão do cromossoma, e levanta muitas questões quanto à organização deste a nível molecular e supramolecular. A sequenciação de alguns genomas veio trazer informação ainda mais pormenorizada sobre esta complexidade.
Figura 8 — Não-proporcionalidade entre os mapas físicos e de ligação (cromossoma e mapa de ligação hipotéticos).