Mendel conseguiu estabelecer as duas leis fundamentais da hereditariedade utilizando materiais precisamente definidos e controlando totalmente os cruzamentos. Na Natureza é diferente: em vez de grupos homogéneos geneticamente, cruzam-se indivíduos heterogéneos; as gerações são, em muitos casos, sobrepostas entre si; mas, sobretudo, o observador não controla os cruzamentos. No caso de plantas com ciclo de vida curto, pode ser relativamente fácil optar-se pela manipulação dos cruzamentos — com fins de melhoramento ou outros — mas noutros casos (designadamente árvores) essa opção não existe, ficando apenas o espaço para a observação passiva, recorrendo aos desenvolvimentos teóricos da Genética de Populações.
Nos casos em que o material de trabalho é geneticamente heterogéneo, a primeira tarefa consiste em determinar as frequências dos genes em cada locus que interesse estudar. A frequência de cada alelo numa população determina-se pela proporção de cromossomas contendo esse alelo. Dado que essa determinação se faz nos esporófitos diplóides, cada indivíduo conta dois cromossomas contendo o locus. Assim, há um total de 2N cromossomas a considerar (para um número N de indivíduos), e a frequência genética para um dado alelo, A por exemplo, é dada pela fórmula
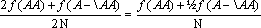
isto é, somando o total de homozigóticos, f(AA), com metade dos heterozigóticos para esse gene, ½f(A– \AA), e dividindo pelo total da amostra. A caracterização genética das populações para um determinado locus requer o conhecimento das frequências de todos os alelos para esse locus, utilizando esta fórmula.
Exemplo
Numa amostra aleatória de 300 indivíduos, dentro de uma dada população, determinaram-se os genótipos em dois loci, tendo-se obtido:
| AABB 5 | AABb 18 | AA'BB 9 | AA'Bb 37 | AaBB 7 | AaBb 29 | f(AA) = 34 | f(BB) = 38 |
| AAbb 11 | AA'bb 28 | Aabb 22 | f(AA') = 74 | f(Bb) = 152 | |||
| A'A'BB 8 | A'A'Bb 31 | A'aBB 8 | A'aBb 30 | f(A'A') = 57 | f(bb) = 110 | ||
| A'A'bb 18 | A'abb 24 | f(Aa) = 58 | |||||
| aaBB 1 | aaBb 7 | f(A'a) = 62 | |||||
| aabb 7 | f(aa) = 15 |
donde resultam as frequências
[(34 + ½(74+58)] ÷ 300 = 0,3(3) = pA (A) | [(38 + ½(152)] ÷ 300 = 0,38 = pB (B) |
|
[(57 + ½(74+62)] ÷ 300 = 0,416(6) = qA (A') | [(110 + ½(152)] ÷ 300 = 0,62 = qB (b) |
|
[(15 + ½(58+62)] ÷ 300 = 0,25 = rA (a) |
No caso de experiências do tipo mendeliano, quer se trate de variação discreta ou contínua, o número de alelos por locus segregante é sempre dois e as suas frequências (desde que a 1ª lei de Mendel se verifique) são exactamente 0,5. A diferença fundamental, ao passar-se para a Genética de Populações, consiste em considerar as frequências dos genes como variáveis, enquanto nas experiências de metodologia mendeliana são constantes (0,5).
A lei de Hardy-Weinberg constitui o sistemático ponto de referência em Genética de Populações e prevê frequências genotípicas iguais aos produtos probabilísticos entre as frequências genéticas respectivas; por exemplo, f(AA)/N = pA × pA, o que quer dizer o seguinte: a probabilidade de encontrar um genótipo AA na população é igual à probabilidade de dois cromossomas tomados ao acaso numa amostragem de gâmetas (um masculino e outro feminino) serem ambos A.
Na nomenclatura aqui utilizada, que define variáveis (p, q, etc.) para cada uma das frequências dos genes, a lei de Hardy-Weinberg determina que as frequências genotípicas respectivas sejam dadas, quando se trate de dois alelos, pelo desenvolvimento do binómio
(p(A) + q(a))2 = p2(AA) + 2pq(Aa) + q2(aa)
Para três alelos, será (p + q + r)2 e assim sucessivamente para quatro, etc.. Note-se que, considerando todos os alelos na população, a expressão obtida tem de totalizar 1, mas considerando apenas um subconjunto dos alelos o mesmo princípio é aplicável e testável estatisticamente.
Exemplo
(continuação)
genótipo | AA | A'A' | aa | AA' | Aa | A'a |
|---|---|---|---|---|---|---|
frequências (modelo H.-W.) | 0,3(3)2 | 0,416(6)2 | 0,252 | 2×0,3(3)×0,416(6) | 2×0,3(3)×0,25 | 2×0,416(6)×0,25 |
valores esperados (N=300) | 33,3(3) | 52,083(3) | 18,75 | 83,3(3) | 50 | 62,5 |
valores observados | 34 | 57 | 15 | 74 | 58 | 62 |
| χ23 = 3,65 | P > 0,25 |
genótipo | BB | Bb | bb |
|---|---|---|---|
frequências (modelo H.-W.) | 0,382 | 2×0,38×0,62 | 0,622 |
valores esperados (N=300) | 43,32 | 141,36 | 115,32 |
valores observados | 38 | 152 | 110 |
| χ21 = 1,70 | P > 0,1 |
Assim, tanto um como o outro locus não parecem afastar-se significativamente do previsto pela lei de Hardy-Weinberg.
Note-se que o número de graus de liberdade leva em conta o estimarem-se 3 parâmetros para o locus A, a partir dos dados, para cálculo dos valores esperados: os valores totais e duas das frequências genéticas (2 parâmetros para o locus B, dado que é só uma frequência, mas continua sem a correcção de 0,5 apesar de ter só 1 g.l.).
Qualquer que seja o número de alelos num dado locus existentes na população, a lei de Hardy-Weinberg prevê frequências genotípicas dependentes apenas das frequências dos genes respectivos. Uma consequência desta lei é que as frequências genotípicas numa determinada geração são o desenvolvimento do quadrado do binómio p + q, ou do trinómio p + q + r, etc., onde figuram as frequências dos gâmetas produzidos pela geração anterior.
Tomemos como exemplo o trinómio (p + q + r)2 = 1. A partir das frequências genotípicas resultantes, que frequências se obtêm? Calculando para o primeiro alelo, tem-se p2 + pq + pr = p(p + q + r) = p, e assim sucessivamente — obtêm-se as mesmas frequências que na geração anterior. As frequências genotípicas expressas neste trinómio, que resultavam das combinações possíveis entre os três tipos de gâmetas com frequências p, q e r, vão na geração seguinte reconstituir os mesmos valores para as variáveis p, q e r (isto é verdade mesmo que a distribuição de frequências genotípicas da geração anterior seja diferente da do desenvolvimento do trinómio, a diferença é que, pelas condições da lei de Hardy-Weinberg, logo na geração seguinte se terá a que é prevista por esta lei). Se não houver qualquer perturbação das condições que permitem a manutenção destes resultados probabilísticos, em cada geração as frequências dos genes vão ser sempre as mesmas. É por isso que a lei de Hardy-Weinberg prevê uma situação de equilíbrio (no sentido em que não variam de geração em geração) das frequências. De certa maneira, é como se disséssemos que as populações herdam, com os genes, as respectivas frequências.
O equilíbrio obtido no modelo de Hardy-Weinberg é probabilístico, sendo exacto apenas quando o desvio-padrão associado às frequências dos genes é nulo; por isso as populações que correspondem a este modelo são infinitamente grandes. Além disso, pressupõe que participam na reprodução apenas os indivíduos da mesma população (por exemplo, não pode intervir pólen de uma população com frequências diferentes, nem encontrarem-se indivíduos que germinaram a partir de sementes que se desenvolveram noutras populações): tais populações são isoladas geneticamente de outras. Finalmente, as frequências dos genes não podem ser alteradas por mutação ou por desvios pré-zigóticos à 1ª lei de Mendel, nem os diferentes genótipos podem participar preferencialmente na reprodução; estas duas últimas condições definem a população como panmíctica, uma população na qual os cruzamentos são feitos ao acaso e com igual fertilidade, e todos os genótipos têm iguais probabilidades de desenvolverem-se, sobreviverem, e participarem na reprodução na geração subsequente.
Pode argumentar-se que estas condições de equilíbrio nunca se verificam; e
no entanto, as observações em populações reais têm demonstrado muitos
exemplos que aproximam suficientemente as previsões da lei de
Hardy-Weinberg. Esta constatação permitiu assumir, em muitos casos de loci
com dominância completa (em que a distinção dos heterozigóticos é
impossível), que a única frequência genotípica observável por par de genes,
a do homozigótico recessivo, se aproximaria de q2, pelo que nas diversas
instâncias se consideraria 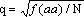 .
.
Exemplo
Uma extensão deste princípio permite a previsão de descendentes com fenótipo recessivo a partir dos três tipos de cruzamentos possíveis (nesta tabela as frequências f são relativas):
Tipo de cruzamento | Proporção (por tipo de cruzamento) de descendentes aa | ||
dominante × dominante | ¼ × f2(Aa) / [1 – f(aa)]2 = | q2 / (1 + q)2 |
|
dominante × recessivo | ½ × f(Aa) × f(aa) / {[1 – f(aa)] × f(aa)} = | q / (1 + q) |
|
recessivo × recessivo | 1 × f2(aa) / f2(aa) = | 1 |
|
Nos numeradores estão os cruzamentos que podem dar descendentes aa (por exemplo o único cruzamento dominante × dominante nessas condições será o Aa × Aa) multiplicados pela proporção de seus descendentes que, pela 1ª lei de Mendel, são aa; no denominador, o total de cruzamentos desse tipo (para o mesmo caso, todos os que são A– × A–). O uso da multiplicação entre as frequências genotípicas implica cruzamentos ao acaso, isto é, panmixia.
Assumindo que a população está em equilíbrio de Hardy-Weinberg, então o número de progenitores com fenótipo recessivo permite deduzir o valor q(a), o qual ao ser introduzido nas fórmulas da coluna da direita fornece uma estimativa que é comparável (inclusivamente com teste χ2) com os descendentes observados com fenótipo recessivo em cada tipo de cruzamento. Requer-se apenas o conhecimento exacto dos tipos de cruzamento. Este teste de Snyder comprova o postulado de q2 ser a proporção de indivíduos aa, na medida em que os valores na descendência só se verificam com cruzamentos ao acaso (representados pelos denominadores à esquerda da igualdade) e a ausência de favorecimento de genótipos (os numeradores respectivos), e é bastante utilizado em estudos na espécie humana. Foi o próprio Snyder que exemplificou com a sensibilidade gustativa à feniltiocarbamida (os indivíduos expressando o gene recessivo são insensíveis), tendo analisado as descendências de 425 cruzamentos dominante × dominante, 289 dominante × recessivo, e 86 cruzamentos recessivo × recessivo, donde se identificaram 130/1059, 278/761 e 218/223 descendentes insensíveis. Os 461 indivíduos homozigóticos recessivos na geração de progenitores, pela lei de Hardy-Weinberg, permitem obter a frequência do gene recessivo, q = √(461/1600) = 0,5368, donde derivam as expectativas de 129,2, 265,8 e 223 descendentes homozigóticos recessivos a partir dos três tipos de cruzamento, pela mesma ordem. A concordância é muito alta, apesar dos 5 descendentes sensíveis no terceiro tipo de cruzamento, fruto talvez de diagnóstico errado num dos progenitores. Usando o teste χ2 com os dados das três classes, confirma-se que o erro é não-significativo (χ21 = 0,68).
O mesmo princípio permite, em séries alélicas muito complexas e com
codominância, determinar a frequência de cada alelo pela fórmula 1 – 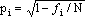 , em que
fi é o número de indivíduos que manifestam um dos alelos (chame-se Ai), ao
qual se refere esta frequência, e por isso contêm pelo menos um gene Ai
observável por causa da codominância.
, em que
fi é o número de indivíduos que manifestam um dos alelos (chame-se Ai), ao
qual se refere esta frequência, e por isso contêm pelo menos um gene Ai
observável por causa da codominância.
É provável que em tais casos os desvios em relação ao ideal, das mais diversas ordens, existam mas acabem por compensar-se mutuamente, resultando a referida aproximação ao modelo; mas o mais importante da lei de Hardy-Weinberg é precisamente servir de "hipótese nula" em termos estatísticos, em relação à qual os dados podem ser testados nos mais diversos problemas. Os parâmetros populacionais que podem alterar as frequências dos genes, como explícito acima, são a dimensão populacional, o contacto genético com outras populações (muitas vezes apelidado de "migração"), a incidência da mutação e da selecção. Nalguns casos, como irá ver-se, geram outros equilíbrios à volta dos quais as frequências genéticas tendem a estabilizar.