Desequilíbrio gamético

Mesmo numa população panmíctica pode existir o que se designa estratificação populacional, isto é, a persistência de heterogeneidades.

Exemplos

a) Imagine-se uma população com 80 indivíduos, os quais se repartem pelos seguintes genótipos:

Neste caso, p_A = q_A = p_B = q_B = 0,5, e as frequências genotípicas correspondem exactamente ao modelo de Hardy-Weinberg. Mais ainda, correspondem exactamente ao desenvolvimento de (p_A + q_A)²×(p_B + q_B)², o que significa que a amostragem gamética é perfeitamente homogénea — que não existe qualquer associação preferencial entre um certo alelo de um locus com um dos alelos do outro locus.

Introduziam-se agora nesta população 20 indivíduos AABB e 20 indivíduos aabb, que iriam participar sem restrições na reprodução, juntamente com os restantes 80, e na geração seguinte, numa amostragem "perfeita" de 180 indivíduos, obtinham-se:

Note-se, que neste caso, os genótipos afastam-se das expectativas da fórmula (p_A + q_A)²×(p_B + q_B)²; por exemplo para AABB, esperar-se-iam 180×p_A²p_B² = 11,25 indivíduos, e não os 20. Embora cada um dos loci esteja em equilíbrio de Hardy-Weinberg, há o que se designa por desequilíbrio gamético, dado que, por via da importação das duas linhas puras, a maior parte dos genes A se encontra associada nos gâmetas com genes B, e reciprocamente a maior parte dos genes a com genes b. Matematicamente, expressa-se este desequilíbrio (d) pela fórmula

d = f(AB)·f(ab) – f(Ab)·f(aB),

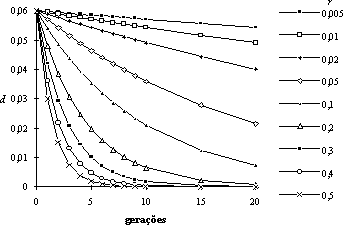
utilizando as frequências relativas dos gâmetas que intervieram na reprodução. Neste caso, obtém-se d = 0,083(3). Assim, apesar da população ser panmíctica, persiste uma estratificação, isto é, há um património genético importado que constitui uma espécie de sub-população que só gradualmente irá homogeneizar-se dentro da população no seu todo. Essa homogeneização depende principalmente da taxa de recombinação entre os dois loci, podendo ser extremamente lenta, especialmente entre loci estreitamente ligados, como ilustra o seguinte gráfico (partindo de um valor inicial d = 0,06):

À persistência de desequilíbrios gaméticos nas populações, em resultado da ligação cromossómica, dá-se o nome de desequilíbrio de ligação.

b) Para os dados dos exemplos anteriores, temos as seguintes frequências gaméticas:

AB: (5 + ½18 + ½9 + ¼37 + ½7 + ¼29)/300 = 0,1283(3)

Ab: (11 + ½18 + ½28 + ¼37 + ½22 + ¼29)/300 = 0,205

A'B: (8 + ½31 + ½9 + ¼37 + ½8 + ¼30)/300 = 0,1625

A'b: (18 + ½31 + ½28 + ¼37 + ½24 + ¼30)/300 = 0,25416(6)

aB: (1 + ½7 + ½7 + ¼29 + ½8 + ¼30)/300 = 0,08916(6)

ab: (7 + ½7 + ½22 + ¼29 + ½24 + ¼30)/300 = 0,16083(3)

f(AB)×f(ab) – f(Ab)×f(aB) = 0,0024,

f(AB)×f(A'b) – f(Ab)×f(A'B) = –0,0007,

f(A'B)×f(ab) – f(A'b)×f(aB) = 0,0035.

os desequilíbrios são muito inferiores a 0,01, mas a havê-los dir-se-á que o gene b tende a estar associado ao gene a, e o gene B, mais ou menos igualmente, aos genes A e A'.

A introdução ("migração") de indivíduos de outras populações constitui por isso um elemento perturbador em relação ao modelo de Hardy-Weinberg, e mesmo que a quebra do isolamento abranja apenas uma geração (o equilíbrio nas novas frequências em cada locus é atingido logo na geração seguinte), gera novos desequilíbrios gaméticos que podem, se entre loci próximos, persistir durante muitas gerações; por isso um grande interesse dos desequilíbrios de ligação reside em assinalarem retrospectivamente eventos de introdução de genes no passado da população. No entanto o facto de a selecção implicar também a criação de desequilíbrios gaméticos, conhecida nomeadamente nas experiências de selecção artificial (cf. "modelo de truncatura"), introduz pelo menos uma segunda maneira de interpretar esses desequilíbrios nas populações naturais, pelo que é necessária alguma cautela.