
Truncar uma distribuição fenotípica é separar um dos seus extremos, isto é, aproveitar para a reprodução apenas os indivíduos cujos fenótipos são os "melhores", portanto os que compõem um determinado percentil p de um dos extremos, rejeitando-se os restantes, figura 16:

Figura 16 — Distribuição fenotípica hipotética de 2000 observações, segundo o modelo normal, indicando a área do percentil de 5% inferior (preenchida com riscas) e os valores X e Z, respectivamente a abcissa e ordenada no ponto de truncatura.
Neste modelo de selecção (o que é mais intuitivo para deslocar a média da população na direcção dos valores perspectivados no programa de melhoramento), e considerando que a distribuição fenotípica é normal, define-se o diferencial de selecção S pela fórmula
S = iσP
ou seja, o desvio-padrão dessa distribuição, σP, afectado de um factor i, a intensidade de selecção. Este i relaciona-se com o inverso do percentil p escolhido para a truncatura: quanto mais reduzida for a percentagem dos "melhores" que se selecciona, mais "intensa" é a selecção.
| p (%) | 50 | 20 | 15 | 10 | 5 | 2 | 1 |
| i | 0,798 | 1,400 | 1,554 | 1,755 | 2,063 | 2,421 | 2,665 |
| X | 0 | 0,842 | 1,036 | 1,282 | 1,645 | 2,054 | 2,326 |
em que X é o valor absoluto do desvio da abcissa em relação à média, em múltiplos de σP. Assim, o valor fenotípico de truncatura para obter um percentil de 5% numa das extremidades da distribuição encontra-se afastado da média em 1,645 vezes o desvio-padrão dessa distribuição.
Exemplo
Achou-se uma variância no teor em alcalóides alucinogéneos numa população
de 2000 plantas de cânhamo de 3,6 × 10–7; seleccionando os 100
indivíduos com valores mais baixos, p = 5% (cf. figura 16), i = 2,063 e o
valor fenotípico máximo entre os indivíduos seleccionados é 1,645 ×  unidades abaixo do valor médio (supondo que a média era 0,003, o valor máximo
seria aproximadamente 0,002).
unidades abaixo do valor médio (supondo que a média era 0,003, o valor máximo
seria aproximadamente 0,002).
|
A tabela dos valores i define-se em função da própria distribuição (cf. figura 16): 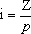 em que p é o percentil escolhido e Z a ordenada da curva N(0, 1) no ponto de truncatura. Em populações cujo efectivo não permita seleccionar percentis estatisticamente grandes, o valor de i é ligeiramente mais baixo que o daquela tabela:
Para estabelecer uma correspondência com a tabela para populações grandes, calcule-se o valor de n/N para ter o valor do percentil p. Os valores em destaque correspondem todos a p = 10%. |
||||||||||||||||||||||||||||||||||||||||||||||||
A resposta à selecção implica uma mudança das características genéticas da população, havendo dois importantes factores em jogo: a selecção propriamente dita, que se expressa na redução da frequência de certos alelos; e a deriva genética, que resulta de se utilizar uma amostra finita (e porventura bastante reduzida) para os cruzamentos.
A selecção tem um efeito previsível sobre frequências dos genes: um alelo A2 cujo efeito médio α2 é no sentido oposto ao da resposta vai tornar-se menos frequente na descendência, e este efeito reflecte-se num coeficiente de selecção que, para o modelo de truncatura, é dado pela igualdade SA2A2 = i × 2a/σP (repare-se que o coeficiente de selecção não é definido como o diferencial de selecção, apesar de serem ambos simbolizados com S). Portanto, quanto maior a diferença entre o valor genotípico dos dois tipos de homozigóticos, maior o efeito da selecção sobre as frequências nesse locus. Desta igualdade se retira que a resposta R, para o conjunto dos loci segregando na população onde se fez a selecção, depende da selecção e da heritabilidade:
R = iVA/σP = h2 × iσP = h2S
A estimativa prévia da heritabilidade permite prever a resposta a obter-se após selecção; na prática, sabendo-se a heritabilidade e o σP pode escolher-se o valor de i que melhor convenha para os resultados pretendidos (mas tendo em atenção os problemas com a deriva genética, v. abaixo).
Podia concluir-se que, no modelo de truncatura pelo menos, o quociente R/S dá uma estimativa da heritabilidade. E de facto, na ausência de estimativas prévias da heritabilidade, os valores R/S podem ser úteis (por exemplo se se pretende fazer um ensaio de pequenas dimensões para projectar um ensaio maior); mas são estimativas a posteriori, ao contrário do conceito fundamental da heritabilidade como estatística a priori. Por isso fala-se de heritabilidade realizada, h2R, para distinguir daquela que se obtém na população onde ainda se pretende seleccionar. A sua determinação pode fazer-se de duas maneiras:
a) medindo, em cada geração, o progresso obtido face à população de base, não-seleccionada (a qual deve ser semeada em simultâneo com todas as gerações seleccionadas para funcionar como verdadeiro padrão), o que pode ter a desvantagem de exigir muito espaço para a manter com Ne elevado;
b) fazendo selecção bidireccional, isto é, mantendo duas populações que são como que a imagem ao espelho uma da outra: em cada geração, todas as manipulações feitas com a população em melhoramento são replicadas numa população à qual se aplica um "anti-melhoramento", com diferenciais de selecção simétricos um em relação ao outro. Neste segundo caso, a heritabilidade realizada será metade do declive da recta representando a diferença acumulada entre as duas variedades seleccionadas simetricamente:
Exemplo
Geração | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
S (±) acumulado | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
R+ (acumulada) | 11 | 15 | 27 | 44 | 43 | 52 | 58 | 71 |
R– (acumulada) | –6 | –21 | –27 | –28 | –46 | –57 | –67 | –72 |
R* = (R+ – R–)/2 | 8,5 | 18 | 27 | 36 | 44,5 | 54,5 | 62,5 | 71,5 |
Como se torna evidente, há flutuações de geração para geração que se devem provavelmente a efeitos ambientais, neste exemplo quase exactamente paralelos entre as duas linhas R+ e R–; por isso a aparente resposta negativa na linha R+, da geração 4 para a 5, não deixa de se reflectir numa R* global da ordem dos 8,5. A regressão de R* em S dá-nos uma estimativa para a h2R:
h2R = bR*S = 0,449
|
Um problema com as estimativas de h2R é o chamado efeito de Bulmer (cf. Falconer e MacKay), que consiste num declínio da VA na primeira geração, tanto mais pronunciado quanto maior seja a heritabilidade para a característica, e que vai recuperando em poucas gerações; a heritabilidade realizada na primeira geração (função da VA na população inicial) não terá por isso grande relevância para prever os resultados na geração seguinte. Este efeito deriva de um desequilíbrio gamético negativo provocado pela selecção, e que pelo menos entre grupos de ligação (cf. "desequilíbrio gamético") é de curta duração, daí resultando a parcial recuperação da VA. |
Os efeitos da deriva genética, imprevisíveis, são fortemente limitantes da intensidade de selecção, isto porque o valor de i é inverso em relação ao percentil utilizado; quanto maior for a intensidade de selecção, menos são os indivíduos utilizados na selecção e maiores os efeitos aleatórios da perda de alelos. A deriva genética pode implicar a perda de alelos que deveriam ser úteis para o melhoramento, deste modo perdendo-se o potencial de melhoramento que havia à partida.
Primeiro que tudo, há que ter a certeza que a população é heterogénea geneticamente, e a medida-padrão dessa heterogeneidade é a heritabilidade. As decisões sobre custos e expectativas de retorno acabam por decidir-se em torno deste parâmetro, e no entanto há que ter em mente o seu reduzido alcance: a heritabilidade limita-se a descrever a geração em que é medida, e pouco ou nada prediz sobre até que ponto pode levar-se a selecção para um dos extremos da distribuição fenotípica — muitas vezes verifica-se que as respostas podem continuar até para além dos valores mais extremos da distribuição inicial.
No caso do cruzamento entre linhas puras, é ainda necessário tomar-se em consideração a possibilidade de grande parte dos genes favoráveis provirem de uma das variedades parentais apenas. Quando isso acontece, a resposta à selecção pode não melhorar muito em relação a este progenitor que à partida "tem tudo" o que interessa no melhoramento. Seleccionar seria uma tarefa fútil nesses casos em que se diz haver associação dos genes favoráveis apenas num dos progenitores. É assim que a escolha das variedades a cruzar tem de fazer-se com base numa certeza de que cada uma tem um substancial contributo genético que é complementar da outra, isto é, quando os genes que o melhorador pretende reunir numa nova variedade estão em dispersão nos progenitores; é na F1 que eles primeiro se reúnem em cada indivíduo, e a tarefa a partir da F2 consiste em seleccionar aqueles que concentram os genes melhores, idealmente sem perder nada do potencial existente à partida.
Preservação da diversidadeO impressionante progresso conseguido nas características das novas variedades saídas de programas de melhoramento não dá sinais de vir a parar tão cedo. Deve-se tal facto à não menos impressionante diversidade genética ainda presente nas populações, assim como ao cuidado que os melhoradores se vêem obrigados a ter de modo a preservar essa diversidade.
Um desses cuidados tem a ver com a aparente interdependência entre certos fenótipos vitais para a sobrevivência e reprodução dos indivíduos. O progresso no melhoramento de um fenótipo traz consigo, muito frequentemente, efeitos adversos de perda de fertilidade ou aumento da letalidade; as causas possíveis são muito diversas, e prendem-se frequentemente com a perda fortuita de genes envolvidos às vezes pleiotropicamente nessas características, seja pela deriva, seja por ligação cromossómica; a vantagem dos heterozigóticos em certos loci pode também implicar um carga genética segregacional decorrente da selecção. No seu conjunto, reflectem uma selecção natural contra os indivíduos seleccionados artificialmente, e requerem medidas de "abertura" da população ou pura e simplesmente um relaxamento da selecção durante uma ou duas gerações.
Trabalhar com populações "fechadas", isto é, começar com uma população-base e produzir uma única linha de melhoramento sem introduzir diversidade por cruzamentos com outras populações é ignorar que os Ne são forçosamente finitos e acabam por ter os reflexos mais imprevisíveis sobre as características das populações que se supõe estarem melhoradas. Duas medidas contrabalançam esses efeitos, e que cabe aos melhoradores saber introduzir na altura certa:
Primeiro, o cruzamento com stocks genéticos diferentes, como que a introduzir "sangue novo" na população; para isso importa ter acesso a um germoplasma capaz de corresponder a estas expectativas (cf. "recursos genéticos") — por outro lado, é uma estratégia que pode acarretar um atraso prolongado na obtenção de novas variedades com interesse;
Segundo, a manutenção em simultâneo de diversas linhas sujeitas ao mesmo procedimento de melhoramento, na expectativa que os efeitos da deriva genética não se repitam exactamente de umas para as outras; deste modo, diversos loci podem ficar fixados numa ou mesmo em todas, mas de maneira diferente de umas para as outras. Por outras palavras, os gâmetas das diferentes linhas tendem a ficar com uma correlação negativa entre si (cf. "consanguinidade"). Cruzando-as entre si, durante o programa de selecção restabelece-se temporariamente um Ne relativamente elevado que permite recuperar muita da diversidade para a nova geração. Equivale isto a dizer que, comparado com um Ne custosamente alto de uma só população, é preferível ter n populações pequenas (Ne/n para cada uma, por exemplo), onde a deriva assume um papel mais preponderante, mas com muito menor risco da perda irreversível de alelos de interesse, que a mutação muito provavelmente não iria repor. Como para tudo, há limites para esta estratégia, dado que a excessiva fragmentação do stock a ser melhorado torna as respostas demasiado imprevisíveis, e aí o progresso do melhoramento dentro de cada linha seria inviabilizado.
Conflitos entre a intensidade de selecção e a fertilidadeDe acordo com a taxa de reprodução, sobretudo com plantas que só se reproduzem uma vez, o percentil da distribuição seleccionado será maior ou menor de maneira a poder repor-se o efectivo da geração anterior. Por isso em certas circunstâncias vale mais não fixar o p e fixar um número mínimo n de indivíduos seleccionados. Mas nesses casos há que perguntar se a selecção está a reduzir a fertilidade dos indivíduos (ver acima), pois pode chegar-se ao absurdo de ter de usar um i demasiado baixo, que não selecciona grande coisa!
|
Além disso, os indivíduos que melhor se reproduzem são aqueles aos quais corresponde um diferencial de selecção mais baixo, e nesse caso interessa calcular a média ponderada do S em função da fertilidade de cada um; pode neste caso concluir-se que com essa população não há mais nada a melhorar. |