Quando a partir de um único heterozigótico se forma um homozigoto, os dois genes deste último são idênticos por descendência: são duas réplicas de um só cromossoma presente no heterozigoto:
| Aa | |||
| gâmetas: | ... A A A A | a a a a ... | |
| | selfing | ||
| AA | aa |
 A probabilidade de ter genótipos idênticos por descendência (AA ou aa)
através de selfing é, pela 1ª lei de Mendel, ¼ + ¼ = ½; mas como será noutros
modelos de cruzamento? Suponhamos um locus A/a, em ligação muito próxima (rAB
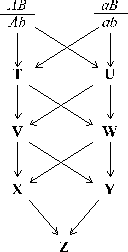
≈ 0) com um locus B/b. O esquema ao lado representa a
sucessão de quatro gerações em que se faz sistematicamente o cruzamento entre
irmãos (T × U, V × W, X × Y), e não há selfing:
A probabilidade de ter genótipos idênticos por descendência (AA ou aa)
através de selfing é, pela 1ª lei de Mendel, ¼ + ¼ = ½; mas como será noutros
modelos de cruzamento? Suponhamos um locus A/a, em ligação muito próxima (rAB
≈ 0) com um locus B/b. O esquema ao lado representa a
sucessão de quatro gerações em que se faz sistematicamente o cruzamento entre
irmãos (T × U, V × W, X × Y), e não há selfing:
Cada seta indica a passagem de um gâmeta. Como é que T e U poderiam ser idênticos geneticamente? Se ambos fossem BB, ou ambos bb. No entanto isto não é ainda identidade por descendência, porque tanto nos BB como nos bb cada gene do locus B/b está ligado a um diferente gene do locus A/a, atestando a sua diferente origem.
Já no indivíduo V existe a possibilidade de exactamente o mesmo cromossoma (um dos quatro presentes nos progenitores iniciais) aparecer duas vezes, para o que se concebem quatro possibilidades:
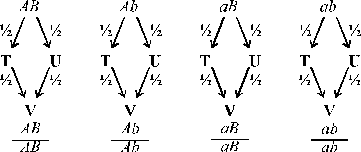
A cada seta, segundo a 1ª lei de Mendel, corresponde uma probabilidade de ½ de o cromossoma em causa ser transmitido à geração seguinte. Daí se conclui que cada uma destas quatro alternativas de identidade por descendência tem uma probabilidade de (½)4 = 1/16; mas como são independentes, a probabilidade de obter identidade por descendência (sem precisar que cromossoma aparece duplicado nesse indivíduo) é globalmente 4×(½)4 = ¼.
Se foram utilizados 4 indivíduos em cada geração (cruzamentos entre primos-direitos), adiando a possibilidade de identidade por descendência para o terceiro cruzamento, tem-se
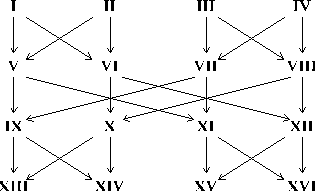
Os progenitores directos do indivíduo XIII (ou de qualquer um dos da quarta geração) contêm em proporção aproximadamente igual a herança dos indivíduos I, II, III e IV. No entanto, pode acontecer identidade por descendência a partir de qualquer dos progenitores, tanto de I via V e IX e via VI e X, como de IV via VII e IX e via VIII e X, etc.. Se os quatro indivíduos iniciais não tivessem parentesco entre si, então existiam à partida 8 cromossomas diferentes por grupo de ligação e a probabilidade de obter-se identidade por descendência na 4ª geração ficava 8×(½)6 = 1/8.
Estes modelos podem ser utilizados na prática em diversos contextos de melhoramento, especialmente para a obtenção de linhas puras mais ou menos aceleradamente: o aumento da percentagem de homozigóticos idênticos por descendência será tanto maior quanto menor o número de indivíduos envolvidos à partida (4, 2 ou 1), isto é, quanto menor a diversidade genética presente de início.
Já com animais de criação, ou no estudo de árvores genealógicas na espécie humana, é mais provável que os esquemas de cruzamento adoptados (ou aparentes) sejam muito irregulares, pelo que se requer o cálculo exacto da identidade por descendência em qualquer situação. Sendo que o parentesco entre os dois progenitores de um indivíduo determina a identidade por descendência que vai recair sobre ele, define-se um coeficiente de parentesco entre progenitores cujo cálculo generalizado tem as seguintes regras:
Regra principal: o coeficiente de parentesco fPQ, entre dois indivíduos P e Q, é a média dos coeficientes de parentesco entre as duas famílias, mais precisamente entre cada um dos progenitores de P e cada um dos progenitores de Q. Assim, na genealogia
| A B P |
C D Q |
fPQ = (fAC + fAD + fBC + fBD)/4 |
Note-se que em certas circunstâncias não se envolvem 4 progenitores diferentes (mais abaixo dão-se alguns exemplos).
Regra auxiliar: o coeficiente de parentesco entre dois indivíduos é igual à média dos coeficientes de parentesco entre um desses indivíduos e cada um dos progenitores do outro. A aplicação desta regra, no caso desta genealogia, mostra que fPQ = (fQA + fQB)/2, fQA = (fAC + fAD)/2, fQB = (fBC + fBD)/2, donde fPQ = (fAC + fAD + fBC + fBD)/4.
Identidade entre gâmetas do mesmo indivíduo: no caso em que P e Q são meios-irmãos, ou seja pondo por exemplo D = A, obtém-se fPQ = (fAC + fAA + fBC + fBD)/4; já se P e Q são irmãos por selfing, é quando A = B = C = D, dando fPQ = 4fAA/4 = fAA. Note-se que aparece um coeficiente de parentesco do indivíduo consigo mesmo (as instâncias de fAA nestes exemplos), e como ele é igual ao coeficiente de parentesco entre irmãos por selfing, tenderíamos a pensar que vale ½ (cf. cálculo feito acima). Mais em rigor, porém, verifica-se que varia entre ½ e 1, em função do coeficiente de parentesco entre os progenitores de A. Para determinar a fórmula geral de fQQ ponha-se A = C, B = D, e P = Q (como se se tratasse do cálculo do parentesco entre dois gémeos monozigóticos); então fQQ = (fCC + 2fCD + fDD)/4, com valores de fCC e fDD exactamente 1, visto que se trata do mesmo par de gâmetas para os dois Qs. Daqui resulta que fQQ = ½ (1 + fCD) isto é, fQQ varia entre ½ e 1 consoante o parentesco entre C e D varia entre 0 e 1.
É comum representar-se fAA = ½(1 + FA), em que FA é o coeficiente de consanguinidade (genealógico) do indivíduo A, definido como a probabilidade dessa identidade por descendência já se encontrar nesse indivíduo, sem especificar os respectivos progenitores. Por outras palavras, FA é numericamente igual ao coeficiente de parentesco entre os progenitores de A.
Estas regras também se aplicam a genealogias regulares como a de Z apresentada acima, onde vigora uma analogia com o modelo A = C e B = D em cada geração. Assim, fTU = ¼, ou seja a identidade por descendência já calculada para qualquer um dos seus descendentes (V e W). Quanto ao valor da identidade por descendência de Z: fVW = (fTT + 2fTU + fUU)/4, e dado que T e U não são consanguíneos, fVW = 3/8 (o coeficiente de consanguinidade de X e também de Y); continuando, fXY = (fVV + 2fVW + fWW)/4 = (½(1 + FV) + 6/8 + ½(1 + FW))/4 = (0,625 + 0,75 + 0,625)/4 = ½ = FZ. De igual modo, para a genealogia dos primos-direitos XIII – XVI, verifica-se que na segunda geração são irmãos dois a dois (V com VI e VII com VIII), dando um fIX,X = fXI,XII = 1/8 = FXIII = FXIV = FXV = FXVI.
Comparando esses dois exemplos com o modelo de selfing, constata-se que, ao fim de 3 gerações, se atingem valores de identidade por descendência de 0,875 no selfing, 0,375 entre irmãos, e 0,125 entre primos direitos. Trata-se de famílias isoladas reprodutivamente, isto é, sem intervenção de indivíduos de outras proveniências, e que em cada geração têm um número fixo de indivíduos utilizados na reprodução, respectivamente 1, 2 e 4. O material de partida, sejam 2, 4 ou 8 cromossomas, é pois o único que pode continuar a considerar-se nas sucessivas gerações. Donde se conclui que quanto menor é o efectivo populacional N (1, 2 ou 4 indivíduos utilizados por geração), mais rapidamente aumenta a proporção de loci idênticos por descendência.
Quando se estudam populações, sem conhecimento dos cruzamentos que contribuem para a geração seguinte, não se pode saber a contribuição em gâmetas de cada progenitor, e é sempre de supor uma desigualdade entre os diferentes indivíduos nesse contributo, mesmo que isso se deva apenas ao acaso. Por isso, o número de indivíduos que participam na reprodução não é representativo da diversidade genética disponível em cada ciclo reprodutor; em lugar do N "demográfico" define-se o tamanho efectivo Ne, que é o número de indivíduos numa população panmíctica, ideal, que produz após a reprodução o mesmo grau de identidade por descendência que a população em estudo. Em geral, o valor de Ne a utilizar é inferior ao N demográfico dessa população.
Numa população com tamanho Ne, a probabilidade dos genes nos gâmetas que se conjugam terem identidade por descendência depende da sua proveniência: no caso ideal (progenitores com F = 0), a identidade por descendência entre os gâmetas é 1/2 se provêm do mesmo indivíduo, e 0 se de indivíduos diferentes. Designando como I a probabilidade de provirem do mesmo indivíduo, obtém-se F = ½I.
Contudo, se os progenitores tiverem F ≠ 0, então a identidade por descendência entre os gâmetas será ½(1 + Fn–1) se provêm do mesmo progenitor, em que n–1 designa a geração dos progenitores, e Fn–1 se provêm de progenitores diferentes. Neste caso, Fn = In[½(1 + Fn–1)] + (1 – In)Fn–1, n designando a geração dos descendentes. Pela definição de Ne, numa população panmíctica In = 1/Ne, donde resulta
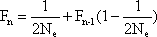
Neste contexto, tem-se um coeficiente de consanguinidade populacional, para distinguir do F genealógico visto anteriormente. Complementarmente a Fn, define-se o índice panmíctico Pn = 1 – Fn donde se extrai
![]()
e, com Ne constante de geração para geração, ![]()
A geração 0 define-se arbitrariamente, como situação de referência para a análise da consanguinidade.
|
Os valores do F genealógico ao fim de 3 gerações, nos pedigrees com cruzamentos entre irmãos (Ne = 2) ou entre primos
direitos (Ne = 4), são inferiores aos do F populacional com Ne igual; em parte isto deve-se ao facto de nunca se considerar
a possibilidade dos gâmetas provirem do mesmo indivíduo. Há uma fórmula de Fn mais geral, embora pouco conhecida, que
leva em conta o Fn-2 e a proporção h de autofertilização: |
Note-se que com a passagem das gerações P irá tendendo para 0. A tabela seguinte mostra, a partir da fórmula de Pn, o número de gerações necessárias a que o valor de Pn fique inferior a 5, 1 ou 0,1%, mesmo partindo de um P0 = 1 (F0 = 0):
P0 = 1 | Ne | ||||||
|---|---|---|---|---|---|---|---|
| Pn | 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
= 0,05 | 5 | 29 | 59 | 299 | 598 | 2995 | 5990 |
= 0,01 | 7 | 44 | 90 | 459 | 919 | 4603 | 9209 |
= 0,001 | 10 | 66 | 135 | 688 | 1379 | 6905 | 13813 |
Por conseguinte, as populações têm Ne finito e a identidade por descendência é uma fatalidade dos mecanismos combinatórios da reprodução sexuada. Haverá populações com uma Ne constante durante longos períodos de tempo? Se bem que as condições ambientais possam variar marcadamente entre ciclos de reprodução sucessivos, com incidências por exemplo no número de indivíduos que se desenvolvem de cada vez em espécies anuais, ou na intensidade de floração feminina em cada ano em espécies perenes, pode assumir-se que essas variações se compensam entre si, resultando um Ne representativo para a população num período de tempo alargado.
Na prática, a variação do valor de F entre duas gerações sucessivas permite, pela própria definição dada acima para Fn, calcular o Ne: 2Ne = (1 – Fn)/(Fn – Fn–1). Para determinar os valores do F populacional em cada geração, recorre-se ao desvio das frequências genotípicas (relativas) em relação os valores esperados segundo o modelo de Hardy-Weinberg. Por exemplo, para um locus A/a, e sem a interferência de outros factores senão o facto da população ser finita, espera-se
f(AA)/N = p2 + pqF f(Aa)/N = 2pq – 2pqF = 2pq(1 – F) f(aa)/N = q2 + pqF |
Neste caso, se na geração n–1 se observassem 250 indivíduos AA, 100 Aa e 50 aa, p(A) = 0,75, q(a) = 0,25, e F = 0,3(3); supondo que na geração n se observavam 255 AA, 90 Aa e 55 aa, o resultado seria um F = 0,4, donde Ne = 5. Note-se que a análise da geração seguinte deve fazer-se de preferência o mais cedo possível no desenvolvimento do esporófito, para minimizar a interferência de mecanismos selectivos que tendam a alterar a distribuição dos genótipos (que geralmente favorecem os heterozigóticos, assim reduzindo a identidade por descendência aparente em fases mais adiantadas desse desenvolvimento).
|
Como o valor teórico dum genótipo homozigótico é o quadrado da respectiva frequência alélica, a proporção total de homozigóticos é o somatório dos valores (pi)2, i = 1, 2, ..., n (número de alelos no locus). Define-se H = 1 – Σi (pi)2 como a proporção téorica de todos os heterozigóticos, e da formulação acima pode deduzir-se que a frequência de heterozigóticos observados é Ho = H(1 – F), donde se calcula o F para qualquer número de alelos. Outras medidas do Ne, que dizem respeito a modelos de reprodução em grupos (nomeadamente de animais submetidos a melhoramento), foram achadas. Por exemplo, acasalando ao acaso Nf fêmeas com Nm machos (estes em número inferior), obtém-se Ne = 4NfNm/(Nf + Nm), ou seja a média harmónica dos valores de Nf e Nm. |
A mutação é um dos mecanismos que contribui, se bem que subtilmente, para impor um limite inferior a 1 ao valor de F. Segundo a Teoria Neutral da variação molecular (cf. "deriva genética"), F tem um valor de equilíbrio F = 1/(1 + θ), em que θ = 4Neu (θ é o chamado parâmetro neutral; u é a taxa de mutação, a partir de qualquer dos alelos, no locus). Este valor indica que, por exemplo para uma população com Ne = 1000, o valor de equilíbrio de F é superior a 0,95 caso a taxa de mutação ronde os 10–5.
Assim supõe-se que as populações com muitas gerações de isolamento num determinado local teriam mais tarde ou mais cedo atingido valores de equilíbrio com a mutação, isto é: só por mutação poderia haver loci em heterozigose. Isto passa-se de facto em espécies que se reproduzem preferencialmente por auto-polinização (Ne ≈ 1, donde em equilíbrio F é quase 1), mas há muitos casos que mostram uma tendência oposta, em que o F se mantém baixo ou é até negativo; isto implica mecanismos de selecção, que nas plantas têm lugar através de mecanismos de auto-incompatibilidade de muitas espécies alogâmicas, ou pela selecção negativa sobre os indivíduos mais homozigóticos.
O valor do F populacional (a partir dos desvios 2pqF em relação às frequências genotípicas dos heterozigotos no equilíbrio de Hardy-Weinberg) pode em alguns loci, por excesso de heterozigóticos na população, ser negativo: isto parece indicar que os gâmetas provenientes da geração anterior tendiam a ser preferencialmente diferentes entre si, nesses loci, e o valor de F descreverá a semelhança estatística entre os gâmetas participantes em cada ciclo reprodutivo em cada locus, e se considerarmos a média dos F em todos os loci analisados como representativa de todo o genoma na população em estudo, definirá uma correlação entre gâmetas:
Exemplo
Considerem-se 4 loci (A–D) com alelos 1 e 0; os seguintes genótipos haplóides ilustram o conceito de correlação entre gâmetas:
locus | A | B | C | D | |
|---|---|---|---|---|---|
gâmeta 1 | 1 | 1 | 0 | 0 | |
gâmeta 2 | 1 | 1 | 0 | 0 | |
F = 1 (gâmetas iguais em todos os loci) |
|||||
gâmeta 1 | 1 | 1 | 0 | 0 | |
gâmeta 2 | 0 | 0 | 1 | 1 | |
F = –1 (gâmetas diferentes " " " loci) |
|||||
gâmeta 1 | 0 | 0 | 1 | 1 | |
gâmeta 2 | 1 | 0 | 1 | 0 | |
F = 0 |
|||||
Sendo F uma medida de correlação, o que significa o valor de referência 0 para populações com Ne finitos? Dado que a conjugação ao acaso tende sempre para um aumento do F em populações finitas, o valor de F = 0 implica por isso que há mecanismos compensatórios desse aumento; então o valor de referência F = 0 não é de facto o do modelo de Hardy-Weinberg, embora coincida com o desse modelo. A existência de tais mecanismos, entre os quais a selecção pré-zigótica (como nos mecanismos de auto-incompatibilidade), a selecção pós-zigótica (por depressão de consanguinidade, cf. secção seguinte) limita-se a produzir uma correlação entre gâmetas numericamente igual, isto é, 0.
|
Quando se comparam as estimativas de F em diferentes loci para uma mesma amostragem de indivíduos, é muito comum que divirjam marcadamente entre si quando a expectativa seria de serem concordantes (o Ne deveria afectar todos os loci de igual maneira). Além da mutação (ver a seguir), o único mecanismo que pode originar estas diferenças entre loci é a selecção. |
Outro factor a levar em conta, especialmente em populações grandes, é a existência de mutações. Em cada locus homozigótico com identidade por descendência, logo que ocorra uma mutação nesse locus num dos homólogos, não só passa a heterozigótico como pode transmitir dois gâmetas diferentes para esse locus se a mutação ocorrer em células percursoras dos gâmetas (recorde-se que nas plantas superiores não há uma separação precoce entre soma e gérmen). Considerando uma população muito grande, com Ne = 104, o acréscimo de 5 × 10–5 no valor de F por geração está na ordem de grandeza de muitas taxas de mutação, que cancelam o aumento do F de tal modo que a correlação entre gâmetas deixa de tender a aumentar nessa população. Este valor de Ne = 104 é assim utilizável como referência para as populações naturais, delimitando duas situações opostas:
a) inbreeding (tendência para a consanguinidade) correspondendo a valores de Ne < 104, sendo que abaixo de 100 já se falaria de inbreeding extremo;
b) outbreeding (tendência para excesso de heterozigóticos), situação com Ne > 104 que é exemplificada não tanto por populações excepcionalmente grandes mas antes pelo cruzamento entre populações muito diferenciadas entre si, designadamente entre subespécies ou mesmo entre espécies.
A correlação negativa entre os gâmetas, em outbreeding, simula um "excedente" de mutação, e de facto a possibilidade de mutações independentes entre duas populações de origem comum enquanto isoladas, ou ainda (talvez mais marcadamente) a de terem estado sujeitas a pressões selectivas diferentes ou aos efeitos da deriva genética, estariam na base da divergência genética entre elas, o que em termos de correlação entre gâmetas iria dar um F < 0 quando de novo reunidas em tais cruzamentos. Neste contexto, o conceito de F como correlação entre gâmetas pode levar, quando se faz outbreeding, ao aparente absurdo de Ne > N.
Quanto maior é uma população, ou mais complexas as interacções entre os indivíduos que a constituem, mais fácil é que haja uma preferência de cruzamento entre indivíduos, não por um factor selectivo em particular mas por outros constrangimentos, por exemplo uma maior probabilidade de cruzamento entre indivíduos geograficamente próximos (isolamento em função da distância), com floração sincronizada (isolamento em função da fenologia da floração) ou (nos humanos) pertencentes a um mesmo clã ou classe social. São populações estratificadas, pois no seu todo não são panmícticas, embora possam sê-lo dentro de cada uma das suas subdivisões (definidas geográfica, fenológica, socialmente, etc.). Essas unidades panmícticas são chamadas demes.
Assim, os valores de Ne são os de cada subdivisão, eventualmente aumentados pela migração entre as subdivisões (fluxo genético intrapopulacional). Em resultado disso aumenta o valor de F, mas não só: associada aos valores baixos de Ne, a deriva genética é um factor importante e resulta numa progressiva diferenciação entre as subdivisões. Uma consequência desta diferenciação é o aumento do F que é medido no conjunto da população, a que se chama o efeito de Wahlund. Esse aumento é proporcional à variância das frequências genéticas dos diferentes estratos.
|
Designando o F de cada subdivisão j como fj, definem-se dois valores de F para uma população estratificada: FIT para o conjunto da população, e um FIS representativo de todas as subdivisões (a média dos fj, o que em rigor só se aplica se todas as subdivisões tiverem o mesmo Ne). O efeito de Wahlund é dado pelo valor FST = (FIT – FIS)/(1 – FIS), derivado da fórmula expressando a relação entre os três, fácil de interpretar em termos de índices panmícticos: PIT = PISPST. Embora a estatística FST seja historicamente importante, e muito utilizada para medir a estratificação intrapopulacional, é preferível recorrer a outra de significado análogo, GST, que não depende da relação entre F e Ne e parte simplesmente das frequências alélicas das subdivisões, ou mesmo outros níveis de comparação, como diferentes populações, diferentes espécies, etc.. Baseia-se na definição HT = HS + DST, em que HS é a média dos valores de heterozigóticos teóricos de cada uma das subdivisões, e DST a grau de diferenciação entre elas. Para todos os pares de subdivisões {X, Y} calcula-se Dxy = (jxx + jyy)/2 – jxy, em que jxx e jyy são os somatórios de homozigóticos teóricos (pi)2, e jxy o somatório dos produtos entre as frequências de cada alelo em X e em Y. DST é a soma de todos os Dxy a dividir pelo quadrado do número de subdivisões. Exemplificando:
Dxy = Dyx = (0,34 + 0,68)/2 – 0,38 = 0,13
JS = (0,34 + 0,68)/2 = 0,51, HS = 1 – JS = 0,49 |
|||||||||||||||||||||||||