(proporções dentro da classe)
(1)
(1/9)
(2/9)
(2/9)
(4/9)
A análise genética requer, como já foi visto, um conhecimento detalhado dos fenótipos e um controlo dos cruzamentos e das condições ambientais. Para a aplicação das leis de Mendel requere-se ainda o trabalho com distribuições discretas (variação descontínua), de tal modo que o agrupamento das observações em classes fenotípicas não seja ambíguo.
O próprio Mendel deixou registado que dentro de cada uma das classes fenotípicas (por exemplo ervilhas amarelas, ervilhas verdes) se notava variação (umas mais amarelas que outras, umas mais verdes que outras), mas qualquer que fosse a semente observada, nunca restariam dúvidas quanto à sua classificação: ou "amarelo", ou "verde". Não importava que dentro destas duas classes houvesse variação, a qual hipoteticamente até teria uma base parcialmente genética (cf. "variação contínua"); importava, sim, a separação entre as duas classes, à qual se atribuiu o efeito de variações genéticas de efeito tão drástico que determinava a descontinuidade entre elas. Em regra, a dedução dos genótipos faz-se sobre estes genes "de grande efeito", e segundo os métodos que a seguir se expõem no caso das plantas.
As distribuições obtidas a partir do selfing de um híbrido fornecem as duas informações fundamentais para a construção de hipóteses genotípicas: o número de classes segregantes e as frequências dessas classes. A teoria exposta nas secções precedentes fornece os modelos genéticos em relação aos quais se pode testar estatisticamente até que ponto se aproximam das observações experimentais; havendo modelos compatíveis com os dados, eles dão uma interpretação dos principais factores genéticos envolvidos. A tabela I resume os exemplos mais comuns onde se aplicam as duas leis de Mendel:
Tabela I
HIPÓTESES GENOTÍPICAS MAIS FREQUENTES
| (a) ênfase para a classe com fenótipo igual ao híbrido progenitor | Nº classes na descendência | Nº de loci segregantes | Interacções alélicas | Interacções não-alélicas | Proporções esperadas(a) |
|---|---|---|---|---|
| 2 | 1 | A dominante | — | 3 : 1 |
| idem (AA letal) | — | 2 : 1 | ||
| 2 | A e B dominantes | A e B redundantes | 15 : 1 | |
| A e B complementares | 9 : 7 | |||
| A epistático (redundante de aabb) | 13 : 3 | |||
| 3 | A, B e C dominantes | A, B e C redundantes | 63 : 1 | |
| 3 | 1 | dom. incompleta, sobred. ou cod. | — | 1 : 2 : 1 |
| 2 | A e B dominantes | A epistático | 12 : 3 : 1 | |
| aa epistático | 9 : 3 : 4 | |||
| A e B complementares e redundantes | 9 : 6 : 1 | |||
| 4 | 2 | A e B dominantes | — | 9 : 3 : 3 : 1 |
| A dominante B/b dom. incompleta, sobred. ou cod. | aa epistático | 3 : 6 : 3 : 4 | ||
| 6 | 2 | A dominante B/b dom. incompleta, sobred. ou cod. | — | 3 : 6 : 3 : 1 : 2 : 1 |
| 8 | 3 | A, B e C dominantes | — | 27 : 9 : 9 : 9 : 3 : 3 : 3 : 1 |
Em geral as hipóteses não vão além dos dois loci por três razões:
i) a dimensão da amostra na descendência pode não ser adequada (por exemplo, para garantir uma probabilidade de mais de 95% de aparecer pelo menos 1 indivíduo para a classe com expectativa 1/64 — como é o caso do triplo recessivo para 3 loci — seriam precisos N ≥ – 64 ln(0,05) ≈ 192 indivíduos);
ii) há maior probabilidade de pelo menos dois dos loci pertencerem ao mesmo grupo de ligação, com o que não se verificaria a 2ª lei (cf. "novos loci", para a metodologia de análise requerida);
iii) havendo segregação independente entre os loci envolvidos e uma amostragem suficiente, pode fazer-se a análise aos loci dois a dois, utilizando os modelos desta tabela, para depois se construir uma hipótese integrada.
Mesmo dentro do limite de dois loci, é relativamente fácil que mais de um modelo genético pareça aplicável aos dados, mesmo após análise estatística (cf. "teste χ2"), visto que as predições dos modelos alternativos são bastante semelhantes entre si (por exemplo entre 3 : 1 e 13 : 3, ou entre 1 : 2 : 1 e 9 : 3 : 4, só uma descendência estatisticamente grande permitiria em certos casos tomar uma decisão segura).
A corroboração de quaisquer modelos, para além da análise estatística, deve ser feita com recurso a cruzamentos envolvendo os indivíduos da descendência, nomeadamente pelo selfing da classe mais frequente ou, quando isso não seja possível na espécie em estudo, pelo testcross (escolhendo para parceiro de cruzamento a classe que o modelo indica como sendo homozigótico recessivo); na falta de melhor, por backcrosses da classe mais frequente aos progenitores ("avós"), se disponíveis.
Exemplo
Um conjunto de híbridos de fenótipo A deu na descendência (F2) três classes: 73 indivíduos de fenótipo A, 30 de fenótipo B, e 29 de fenótipo C. Segundo o modelo de 1 locus, tanto o fenótipo B como o C correspondem a linhas puras; segundo o modelo de 2 loci com epistasia dum gene recessivo, todas as classes da descendência seriam heterogéneas.
Do selfing da classe da F2 com fenótipo A, teríamos duas expectativas:
| 1 locus | 2 loci | ||||||
genótipos da classe mais frequente na F2 (proporções dentro da classe) | Aa (1) | AABB (1/9) | AaBB (2/9) | AABb (2/9) | AaBb (4/9) | ||
Nº de fenótipos segregantes (F3) | 3 | 1 | 2 | 2 | 3 | ||
frequência do fenótipo A (F3) | ½ | 1 | ¾ | ¾ | 9/16 | ||
A inferência estatística é o que permite obter uma medida da aproximação de um modelo genético aos resultados experimentais. Caso os números da descendência do híbrido sejam suficientemente grandes para existirem representantes de todas as classes, e se possível em quantidade dentro de cada uma (o que é em todo caso desejável, dentro dos limites logísticos existentes), o teste χ2 permite tomar decisões que se baseiam na rejeição das hipóteses que se afastam dos dados de tal modo que o erro dessa decisão de rejeitar se considera insignificante.
A fórmula da estatística χ2, para k classes previstas no modelo genético, é
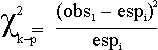
Cada parcela compara um valor observado (o número de ocorrências na respectiva classe fenotípica) com um valor esperado (o número de ocorrências previstas no modelo para essa mesma classe). Ao número de classes, k, subtrai-se o número p de parâmetros que têm de ser calculados a partir das observações, para obter a série de valores esperados. O valor de k-p é número de graus de liberdade da distribuição χ2 a utilizar. Neste contexto, o único parâmetro que os modelos genéticos requerem é a dimensão N = Σobsi da amostra, por isso p = 1.
O total do somatório corresponde a um intervalo na linha com k–1 graus de liberdade da tabela χ2, e por sua vez a um intervalo de probabilidade. Quanto maior for o desvio no numerador de cada parcela, mais provável é que a hipótese configurada no modelo genético proposto para esse teste seja falsa. Por outras palavras, quanto maior for o afastamento entre os resultados observados e as expectativas de um dado modelo, mais remota é a possibilidade de se errar na rejeição desse modelo. Só que, pelo menos em teoria, não é impossível que um erro desses ocorra, e por isso fixa-se um valor de significância como referência para as decisões a tomar: se a probabilidade lida na tabela (correspondente ao erro em se rejeitar a hipótese) estiver abaixo do valor pré-determinado para a significância, a hipótese é rejeitada, à luz dos resultados que se dispõe na série de "observados". Normalmente esse valor não vai acima dos 5%, e se a amostragem for suficientemente grande, pode fixar-se uma significância mais baixa, como 1% ou mesmo 0,1%.
|
Uma maneira intuitiva de organizar os valores para o cálculo do χ2 é através duma tabela onde os sucessivos passos do cálculo ficam esquematizados. Assim, o teste à hipótese 9 : 3 : 3 : 1 para os valores 76 : 38 : 31 : 6
Cada classe corresponde a uma linha, que produz na última coluna uma das parcelas do χ2, isto é, o quadrado do desvio obs–esp a dividir pelo valor esperado respectivo. A obtenção dos totais das colunas é um meio de confirmar a exactidão dos cálculos dos valores esperados e dos desvios Está disponível uma folha de cálculo onde se podem introduzir os valores e obter automaticamente o resultado do teste. |
Quando há apenas duas classes fenotípicas para testar, aplica-se uma correcção de 0,5 ao desvio entre observado e esperado em cada uma das duas parcelas:

como os termos em módulo são iguais entre as duas parcelas, basta utilizar um dos pares {observado, esperado} simplificando-se esta fórmula para
χ21= (|obs – esp| – 0,5)2 × N/(esp1×esp2)
em que N = esp1 + esp2 é o número de observações na amostra.
Uma ressalva importante é este teste perder o seu valor decisório se alguma das classes tiver uma frequência esperada inferior a 5. Nesse caso é preferível perder 1 ou mais graus de liberdade e agrupar classes.
Exemplo
Cruzaram-se duas linhas puras de milho, uma com cutícula brilhante nas folhas e outra com cutícula baça. A F1 era de cutícula brilhante, e dela obtiveram-se 2623 plantas F2, das quais 1980 eram como a F1 e 643 tinham cutícula baça. Neste exemplo iremos testar para estes dados todos os modelos de 2 classes da tabela I:
| Modelo | Valores esperados | χ21 | P |
|---|---|---|---|
3 : 1 | 1967,25; 655,75 | 0,31 | > 0,5 |
2 : 1 | 1748,67; 874,33 | 91,41 | < 0,001 |
15 : 1 | 2459,06; 163,94 | 1490,11 | < 0,001 |
9 : 7 | 1475,44; 1147,56 | 393,61 | < 0,001 |
13 : 3 | 2131,19; 491,81 | 56,83 | < 0,001 |
(NOTA: a apresentação dos valores aproximados às centésimas não implica que os cálculos fossem feitos com aproximações, e é obrigatório que, dentro dos limites a que vão as calculadoras ou folhas de cálculo, se evite a propagação dos erros nas operações por causa de aproximações prévias)
Usando uma significância de 5%, todas as hipóteses menos a primeira (variação fenotípica devida a um único locus em que o alelo que determina cutícula brilhante é dominante) puderam ser rejeitadas: os erros dados pela distribuição χ2 eram insignificantes.
Como tudo em estatística, a capacidade de decisão é tanto maior quanto maior (e mais cuidadosa) for a amostragem; suponhamos que as duas classes da F2 continham apenas 20 e 6 plantas (aproximadamente 100 vezes menos que na F2 anterior, respectivamente). Os cálculos então dariam:
| Modelo | Valores esperados | χ21 | P |
|---|---|---|---|
3 : 1 | 19,50; 6,50 | 0,00 | > 0,995 |
2 : 1 | 17,33; 8,67 | 0,81 | > 0,25 |
15 : 1 | 24,38; 1,62 | 9,91 | < 0,005 |
9 : 7 | 14,62; 11,38 | 3,72 | > 0,05 |
13 : 3 | 21,12; 4,88 | 0,10 | > 0,75 |
Aqui, só uma das hipóteses seria rejeitada (mas com um valor esperado 1,62), deixando em aberto os outros quatro modelos genéticos. O facto de entre estes haver diferenças de probabilidade não é relevante, visto que a decisão estatística se baseia na comparação com uma significância (5%) pré-determinada (a priori pelo menos, a distribuição das observações por classes seria diferente numa amostragem independente desta, e os valores de P já não seriam os mesmos para todas as hipóteses em jogo). Enfim, neste exemplo, para poder rejeitar nem que fosse a hipótese de letalidade, teria de utilizar-se uma significância da ordem dos 37%, que como se compreende faria pouco sentido. Com uma amostragem tão pequena não se decide nada.
É evidente que um certo grau de intuição permite, de um relance sobre os dados, supor qual seja o modelo mais ajustado, pelo que na prática apenas se testam um ou dois; também, na dúvida entre dois modelos não rejeitados, e enquanto não surge uma confirmação experimental mais segura, se pode ter como provisória a preferência daquele que for mais simples. Mas importa sempre ter presente a variedade de modelos genéticos possíveis, e que nenhum deles é aceitado, mas sim todos os outros têm de ser rejeitados.
|
As limitações da aceitação de um modelo podem ainda apresentar-se de outras maneiras: imagine-se que o homozigótico aa de qualquer dos modelos 9 : 3 : ... de di-hibridismo era letal: então aceitar-se-ia o modelo 3 : 1 de mono-hibridismo, estando a supor-se que a classe com ¼ de frequência seria linha pura. Novamente, só pelos cruzamentos se obtém a evidência do gene letal a: fazendo o selfing de cada indivíduo dessa classe (A-bb), seria possível comparar a fertilidade entre os 2/3 de portadores do gene letal a (Aabb) e os 1/3 de não-portadores (AAbb), esperando-se uma produção de apenas ¾ das sementes por flor nos primeiros em relação aos segundos (verificável pelo teste t de comparação entre médias). Caso não fosse possível o selfing, só com loci marcadores (cf. "novos loci") |