O melhoramento de organismos com interesse agronómico visa a satisfação de
necessidades alimentares e/ou económicas e tem sido praticada desde o início
da agricultura. Procede caso a caso segundo duas condicionantes: os
objectivos a atingir por um lado, e os materiais disponíveis (biológicos assim como
logísticos) por outro. Se os fenótipos que interessa melhorar têm
uma variação do tipo mendeliano na população com que se trabalha, torna-se
possível isolar classes genotípicas e a partir destas seleccionar linhas
puras (cf. "leis de Mendel"). É esse o caso de alguns caracteres de
pigmentação (por exemplo, para plantas ornamentais) ou de resistência a
doenças infestantes. No entanto, a maior parte das características com
interesse agronómico têm uma variação de tipo contínuo, onde não há a
possibilidade de isolar os efeitos de cada locus e portanto deixam de poder
determinar-se genótipos. Sabe-se que os mecanismos da meiose actuam
exactamente da mesma maneira para a segregação entre alelos e entre grupos de
ligação que determinam estas características, mas as distribuições
fenotípicas não são adequadas à análise mendeliana. São estes os chamados
"caracteres quantitativos", a designação que é vulgarmente utilizada para
identificar dois tipos de fenótipos:
i)características de variação contínua em sentido estrito: dimensões, pesos, quantidades, tempos/ durações, tudo o que pode ser medido e portanto ter qualquer valor numa escala de números reais;
ii)características de variação descontínua assimilável a uma distribuição contínua: número de grãos por maçaroca, número de nós do caule, número de raízes laterais, tudo o que pode ser contado e portanto ter qualquer valor numa escala de números naturais. Neste caso, cada valor não representa uma classe genotípica por si mesmo, é apenas a manifestação de um fenótipo descontínuo com uma distribuição contínua subjacente. É o "aspecto" da distribuição que, por não mostrar subdivisão da população em classes mais ou menos descontínuas, determina o tratamento destes fenótipos como "caracteres quantitativos".
|
A designação "quantitativo" é imprópria porque os fenótipos com distribuições descontínuas (cf. "relações de dominância") não deixam de ser quantitativos; de facto, a observação de qualquer tipo de fenótipo é quase sempre traduzível em termos quantitativos. Não é por serem "quantitativos" que o tratamento dos fenótipos de variação contínua recebem um tratamento diferente, mas sim pelo tipo de distribuição que apresentam. |
Uma distribuição contínua tem dois parâmetros fundamentais: um valor central e um valor de dispersão. No caso da distribuição normal, que é (felizmente!) aquela que melhor aproxima quase todas as distribuições relativas a fenótipos de variação contínua (cf. "transformações de escala"), o valor central é a média e o valor de dispersão é o desvio-padrão:
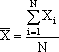 média da variável X tomada de uma amostra de N elementos;
média da variável X tomada de uma amostra de N elementos;
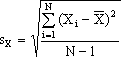 desvio-padrão da variável X tomado de uma amostra de N elementos.
desvio-padrão da variável X tomado de uma amostra de N elementos.
O termo no interior da raiz quadrada tem o nome variância e representa-se por s2X, σ2X, ou simplesmente VX, conforme o contexto.
Exemplo
Mediu-se o crescimento de 14 plântulas de sobreiro, em viveiro, em vasos contendo ou não um fungo micorrízico. Os resultados obtidos foram:
| sem fungo | com fungo | sem fungo | com fungo | |
| 6,3 | 7,9 | |||
| 7,4 | 9,1 | dimensão da amostra | 6 | 8 |
| 4,4 | 11,6 | margem de variação | 4,4 – 7,4 | 5,9 – 11,6 |
| 5,8 | 5,9 | média | 6,167 | 8,375 |
| 6,1 | 9,3 | desvio-padrão | 1,048 | 1,741 |
| 7,0 | 6,7 | |||
| 7,9 | ||||
| 8,6 |
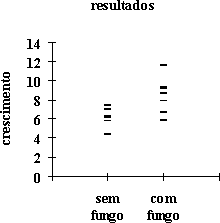 O gráfico respectivo (v. figura à direita) demonstra que dentro de cada
uma destas amostras não se definem classes de valores inequivocamente
separáveis; também evidencia que os valores centrais de cada uma são
diferentes entre si, nomeadamente que o crescimento tende a ser maior na
presença do fungo. Mas as amostras são pequenas e as margens de variação
sobrepõem-se: colocando a hipótese dessa diferença dever-se ao acaso das
amostragens, verifica-se a significância dessa diferença recorrendo à
estatística t. Assumindo que têm a mesma variância (isto é, que os
desvios-padrão calculados são estimativas de um mesmo valor teórico),
então
O gráfico respectivo (v. figura à direita) demonstra que dentro de cada
uma destas amostras não se definem classes de valores inequivocamente
separáveis; também evidencia que os valores centrais de cada uma são
diferentes entre si, nomeadamente que o crescimento tende a ser maior na
presença do fungo. Mas as amostras são pequenas e as margens de variação
sobrepõem-se: colocando a hipótese dessa diferença dever-se ao acaso das
amostragens, verifica-se a significância dessa diferença recorrendo à
estatística t. Assumindo que têm a mesma variância (isto é, que os
desvios-padrão calculados são estimativas de um mesmo valor teórico),
então
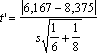 =2,741 > 2,179 = t0,05 (6 + 8 – 2 = 12 g.l.)
=2,741 > 2,179 = t0,05 (6 + 8 – 2 = 12 g.l.)
em que 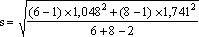 = 1,492
= 1,492
donde se conclui que a diferença entre as médias é significativa, e portanto trata-se de distribuições diferentes, isto é, o seu valor central, indicativo da tendência geral dos valores de crescimento, é diferente consoante o fungo micorrízico está presente ou não.
Toda a variação fenotípica, ou seja, a dispersão dos valores individuais representados numa distribuição, depende em princípio de dois factores: as diferenças entre os genótipos dos indivíduos relevantes para o fenótipo em causa, e as diferenças entre as influências ambientais para a expressão desses genótipos. Assim, pode dizer-se que o fenótipo P de cada indivíduo resulta do seu valor genotípico G e da influência (E) que o ambiente teve sobre a manifestação deste último:
P = G + E
Por exemplo no gráfico precedente, dentro de cada grupo de plântulas de sobreiro há uma dispersão de valores; sem outros dados, elas devem-se em princípio a diferenças de valores genotípicos e de influências ambientais relativos ao fenótipo em estudo (crescimento); já entre os dois grupos (representados pelas respectivas médias) pôde atribuir-se a diferença, pelo design experimental, a um factor ambiental: a associação micorrízica. Experiências adicionais seriam necessárias a verificar se a diferença entre as duas médias era exclusivamente uma diferença entre os tratamentos, isto é, se os dois grupos tinham valores genotípicos médios iguais.
Há uma diferença importante entre as duas componentes da variação fenotípica: só a componente genotípica é em rigor hereditária, e por isso só seleccionando diferenças genotípicas poderá esperar-se um melhoramento de carácter permanente no fenótipo; assim, continuando no mesmo exemplo, a diferença entre grupos foi identificada como ambiental e por isso não é utilizável no melhoramento genético: se se reproduzirem os dois grupos separadamente e as respectivas descendências crescessem em condições iguais, a diferença observada na geração anterior provavelmente desapareceria; mas se as diferenças dentro de cada grupo fossem pelo menos em parte de carácter genotípico, então a selecção dentro de cada grupo poderia resultar numa geração com um comportamento "melhorado".
Tal como na análise mendeliana, a informação àcerca das características genéticas de cada indivíduo é feita retroactivamente, ou seja, é a partir dos fenótipos da respectiva descendência que se deduz tal informação. Em geral — até porque não compensa a avaliação de todos os indivíduos disponíveis — faz-se uma selecção dos que "mais provavelmente" darão descendências que correspondam aos objectivos pretendidos, apesar dos efeitos mais ou menos incontroláveis da componente ambiental. Tais indivíduos normalmente apresentam um fenótipo mais próximo desses objectivos.
Exemplo
(segundo Strickberger, e Mather e Jinks)
Em 1915, East realizou um cruzamento entre duas espécies de Nicotiana caracterizadas pelas diferenças de comprimento das corolas:

A distribuição da F1 poderia ser compatível com um modelo de mono-hibridismo com dominância parcial, mas a da F2 revela que o seu hibridismo é muito mais complexo, o que é patente no facto de praticamente nenhum indivíduo dessa geração ter fenótipo semelhante ao de qualquer das linhas parentais. De facto, podemos até fazer um cálculo do limite inferior ao número k de loci a segregar independentemente na F1 (cf. "selfing") a partir da desigualdade
4–k < 1/444
em que 444 é o número de indivíduos observados na F2. Neste exemplo, k > 4 loci. Por via da recombinação na meiose, produziu-se uma F2 muito complexa genotipicamente (mais de 3k genótipos diferentes) ou seja uma muito maior dispersão de valores genotípicos do que em qualquer das gerações anteriores. A evidência disso mesmo está no acentuado achatamento da distribuição fenotípica dessa F2, quando comparada com as das duas espécies e da F1.
Para confirmá-lo, East realizou a auto-polinização de vários indivíduos da F2, obtendo famílias F3 com valores médios semelhantes aos desses indivíduos F2:
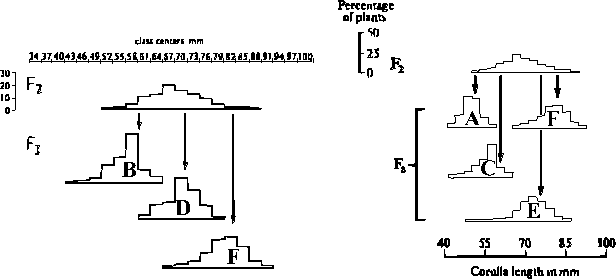
Estes resultados demonstram que diferentes indivíduos da F2 possuem diferentes genótipos para a característica em causa, pois produzem descendências diferentes.
A experiência de East ilustra dois conceitos fundamentais ao estudo da variação contínua: o de resposta à selecção (R) e o de regressão (b).
Os indivíduos seleccionados na F2 tinham fenótipos diferentes da média da população donde foram retirados. Essa diferença é um diferencial de selecção (S), que, na medida em que houve uma resposta R (o afastamento da média da respectiva F3 em relação à média da F2) também representaria uma diferença de conteúdo genético. Por outras palavras, as famílias F3 tinham médias diferentes da média da F2 porque descendiam de indivíduos dessa F2 que se distanciavam geneticamente dessa média. Assim, embora R e S se baseiem em medições fenotípicas, eles estão relacionados entre si pela componente genética que determina a média de cada F3, isto é, os genes transmitidos pelo respectivo progenitor retirado da F2.
Recapitulando para os exemplos ilustrados, temos os seguintes parâmetros:
Exemplo
(continuação)
média da F2 (± desvio-padrão) | 68,86 ± 6,93 | |||||
família | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
fenótipo do progenitor seleccionado | 52 | 59,5 | 61 | 71,5 | 76 | 82 |
diferencial de selecção S | –16,86 | –9,36 | –7,86 | +2,64 | +7,14 | +13,14 |
fenótipo médio da F3 | 50,24 | 56,10 | 55,83 | 70,06 | 72,33 | 80,02 |
resposta R | –18,62 | –12,76 | –13,03 | +1,2 | +3,47 | +11,16 |
Assim, em termos práticos, quando se seleccionam os "melhores" indivíduos numa F2 está-se a aplicar um diferencial de selecção (S), esperando-se uma correspondente resposta (R), em princípio do mesmo sinal, que reflecte o progresso fenotípico da selecção, de uma geração para a outra.
A relação de parentesco implica uma dependência da descendência no
progenitor; por exemplo o progenitor da família A, na experiência de East,
teve uma descendência cujo valor médio 50,24 era correlacionado com o seu
próprio fenótipo 52. Esta interdependência pode variar em maior ou menor
grau, e é expressa pela regressão, uma medida para a dependência estatística
dos valores médios das descendências (Y) em relação aos fenótipos dos
respectivos progenitores (X), sendo definida pela fórmula 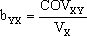 ,
dizendo-se "regressão de Y em X" porque é Y que depende de X (variável
independente), e em que VX é a variância de X (computacionalmente igual ao
quadrado de SX definido anteriormente) e
,
dizendo-se "regressão de Y em X" porque é Y que depende de X (variável
independente), e em que VX é a variância de X (computacionalmente igual ao
quadrado de SX definido anteriormente) e
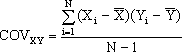
(aqui a ordem de X e Y é indiferente).
O valor de bYX é o declive da recta de regressão de Y em X, em que Y toma os valores de todos os descendentes para cada valor de X (do respectivo progenitor).
A figura 15 ilustra um exemplo muito mais exaustivo de distribuição dos valores médios das descendências em função da distribuição dos valores nos progenitores, onde também é patente o progresso que se obtinha (ou não) pela selecção de algumas famílias.
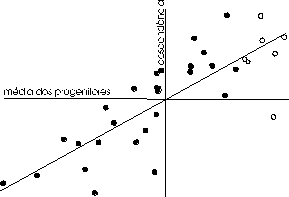
Figura 15 — Regressão do comprimento da asa de Drosophila melanogaster (segundo Falconer e MacKay). Nas abcissas representa-se o valor intermédio de cada par de progenitores, (fêmea + macho) ÷ 2, e nas ordenadas a média das respectivas descendências. A origem dos eixos é a média da população donde se fez a amostragem dos progenitores. A recta de regressão foi sobreposta aos dados e tem um declive bYX = 0,58 ± 0,07. Os pontos a branco representam a selecção dos 7 valores X mais elevados, que projectados sobre o eixo Y ilustram a resposta resultante.
|
A correlação (entre um progenitor e um descendente) é uma medida aparentada com a regressão pela fórmula matemática (rXY = COVXY/(sXsY)), mas tem um significado estatístico muito diferente. Historicamente, precedeu a regressão no estudo da interdependência entre valores biométricos de indivíduos aparentados (pai-filho, irmãos, etc.) na espécie humana. Aplica-se mais propriamente a esse tipo de dados na medida em que, a cada valor de X corresponde um só valor de Y, ou poucos, de tal maneira que se podem considerar duas distribuições normais e a nuvem de pontos formados pelos pares {X,Y} uma variável binormal. Neste tipo de distribuições, considera-se que r2 é proporcional à heritabilidade. |