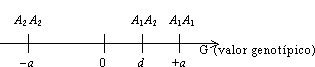
Do empirismo experimental à capacidade de fazer previsões tem de passar-se por um desenvolvimento teórico. Os modelos genéticos para a variação contínua assumem que um número indeterminado de loci se encontram em segregação na meiose, sendo o contributo da variação alélica em cada locus relativamente pequeno em relação ao desvio-padrão da distribuição fenotípica. Diz-se assim que a hereditariedade neste tipo de distribuições é poligénica.
A partir das leis de Mendel pode deduzir-se a contribuição genética dos progenitores para os fenótipos da descendência, isto é, constroem-se modelos genéticos explicativos das respostas à selecção e/ou regressões, assim como a outros resultados experimentais com características de variação contínua. No modelo que irá ser desenvolvido aqui, assume-se que cada um desses loci segrega apenas dois alelos, por exemplo A1/A2, B1/B2, etc.; a cada um dos três genótipos, e para cada locus, corresponde um desvio positivo ou negativo referenciável ao valor intermédio entre os dois homozigóticos (cf. figura 1, "relações de dominância"):
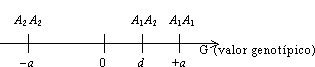
As grandezas a e d são, junto com as frequências p (de A1) e q (de A2), os parâmetros genotípicos e populacionais que servem para descrever o efeito do locus A1/A2 na variação dos valores genotípicos G. Note-se que se atribui a frequência p ao alelo cujo homozigótico tem maior valor na escala fenotípica; é uma convenção que não implica ser esse um alelo dominante. O ponto de referência de valor 0 tem, na generalidade dos casos, um interesse meramente teórico e não é, senão em casos particulares, a média da distribuição fenotípica (M). Esta obtém-se como
M = p2a + 2pqd – q2a
ou, após rearranjo,
M = (p – q)a + 2pqd
(ainda por uma questão de simplicidade, considera-se que a população se encontra em equilíbrio de Hardy-Weinberg, e assume-se que a distribuição dos efeitos ambientais tem média 0, isto é, que a média fenotípica é igual à média dos valores genotípicos)
|
Alguns casos particulares:
|
Dentro da população, continuando neste modelo, há dois tipos de gâmetas por locus segregante. Assim, os genótipos que os gâmetas contendo A1 produzem na geração seguinte não são exactamente os mesmos que os dos restantes gâmetas (contendo A2), resultando descendências diferentes em função duns e doutros:
| gâmeta | frequência | descendência que produz | valor genotípico médio da descendência |
|---|---|---|---|
| A1 | p | pA1A1 + qA1A2 | pa + qd |
| A2 | q | pA1A2 + qA2A2 | pd – qa |
Imaginando uma situação em que apenas pólen de tipo A1 fosse participar na reprodução, esperar-se-ia que o M da geração seguinte fosse diferente do original. É assim que, subtraindo-se à coluna da direita a fórmula de M acima, se obtém o efeito médio (símbolo α) de cada um dos alelos:
|
αA1 = pa + qd – M = q[a + (q – p)d] = qα αA2 = pd – qa – M = –p[a + (q – p)d] = –pα |
O termo no parêntesis recto, α = αA1 – αA2, designa-se por efeito médio de substituição de um alelo pelo outro alelo, em qualquer direcção. O efeito máximo de substituir um gene pelo outro é quando o gene que entra a substituir for raro (é outra maneira de dizer que o efeito da substituição de, por exemplo, A2 por A1, αA1 = qα, é proporcional a q, o valor da frequência do gene substituído). Assim, se pela selecção estivermos a aumentar a frequência de um alelo à custa da frequência do outro alelo, a média da descendência vai reflectir essa alteração numa fracção de α, isto é: a resposta à selecção é uma função do efeito médio de substituição. Somando os efeitos médios dos genes de cada genótipo progenitor, encontram-se os respectivos valores melhoradores:
Genótipo | A1A1 | A1A2 | A2A2 |
Valor melhorador (A) | 2α1 = 2qα | α1 + α2 = (q – p)α | 2α2 = –2pα |
Por causa de adicionarem-se os efeitos médios dos dois genes de cada indivíduo se diz que o valor melhorador de cada genótipo é a componente aditiva (A) do valor genotípico G. A diferença entre G e A é o chamado desvio de dominância D (que é definido em termos populacionais, portanto diferente do parâmetro d). A seguinte tabela resume estas três componentes, uniformizando-as todas em função da média da distribuição fenotípica, M:
Genótipo | A1A1 | A1A2 | A2A2 |
|---|---|---|---|
Valor genotípico (G) | a – M = 2q(a – qd) | d – M = (q – p)a + 2pqd | –a – M = –2p(a + pd) |
Valor melhorador (A) | 2qα | (q – p)α | –2pα |
Desvio de dominância (D) | –2q2d | 2pqd | 2p2d |
|
Note-se que os valores de D não dependem de a. Se o parâmetro d for nulo (ausência de interacção entre alelos), então G = A (variação genotípica "aditiva") e α = a. Esta dedução não se aplica em rigor quando se trate de séries alélicas, pois pode não haver um único valor de referência 0. A formulação matemática é muito diferente, mas verifica-se que os resultados, em termos de covariâncias genotípicas (ver adiante), são os mesmos. Quanto aos problemas da interacção entre loci e desvios em relação ao equilíbrio de Hardy-Weinberg (nomeadamente um coeficiente de consanguinidade F ≠ 0) serão tratados mais adiante. Em todo o caso, são numerosos os resultados experimentais que se conhecem a darem a indicação que, na prática, não existe um erro de maior em assumir para cada locus a formulação exposta. |
Fazendo-se o somatório das contribuições de todo o conjunto de k loci segregando para o fenótipo em estudo, obtêm-se
.gif)
e os valores de G = A + D para cada indivíduo. Como se desconhece o genótipo desse indivíduo e por isso em que loci se aplica a expressão 2qiαi, ou (qi – pi)αi, ou –2piαi, a formulação exacta de A (assim como as de G e D) é sempre uma incógnita. Só empiricamente, pela média dos descendentes de diferentes indivíduos, se podem avaliar os valores de uns em relação aos outros.
Neste ponto importa sobretudo reter a noção que, dentro de uma distribuição fenotípica pode existir uma distribuição de valores melhoradores, os quais dependem dos parâmetros ai, di, pi e qi para cada locus i segregante nessa distribuição; a selecção entre diferentes valores de A é o princípio em que se baseia o melhoramento por selecção.
Interacções entre lociQuando haja interacções entre os loci segregando para uma característica, sejam elas de complementaridade, redundância, epistasia, ou ainda ligação genética, o valor genotípico pode não ser exactamente A + D, definindo-se neste caso uma terceira componente do valor genotípico G, a componente de interaccção, I = G – (A + D).
Exemplo
(segundo Falconer e MacKay)
Recordando o exemplo da pigmentação em murganhos (cf. "genes pleiotrópicos"), suponhamos uma população em equilíbrio de Hardy-Weinberg com 40% de indivíduos de genótipo bb e 20% de genótipo cece:
Classes genotípicas | B–C– | B–cece | bbC– | bbcece |
|---|---|---|---|---|
nº médio de grânulos de melanina | 95 | 38 | 90 | 34 |
tamanho médio dos grânulos | 1,44 | 0,94 | 0,77 | 0,77 |
Designando o fenótipo número de grânulos de melanina por X e o tamanho médio desses grânulos por Y, e assumindo equilíbrio entre os loci, temos as médias globais
MX = 0,48×95 + 0,16×38 + 0,32×90 + 0,08×34 = 83,2
MY = 0,48×1,44 + 0,16×0,94 + (0,32+0,08)×0,77 = 1,112
e os valores genotípicos por cada classe fenotípica, em referência a essas médias,
Classes | B–C– | B–cece | bbC– | bbcece |
|---|---|---|---|---|
GX | 95 – 83,2 = +11,8 | –45,2 | +6,8 | –49,2 |
GY | 1,44 – 1,112 = +0,328 | –0,172 | –0,342 | –0,342 |
e através dos quais se podem obter os valores genotípicos em cada locus:
Classes | B–C– | B–cece | bbC– | bbcece |
|---|---|---|---|---|
GX | 0,8×11,8 + 0,2× – 45,2 = +0,4 | –4,4 | 0,6×11,8 + 0,4×6,8 = +9,8 | –46,8 |
GY | 0,8×0,328 + 0,2× – 0,172 = +0,228 | –0,342 | 0,6×0,328 + 0,4×–0,342 = +0,060 | –0,240 |
Os valores de A + D para cada classe (B–C–, etc.) são dados pela soma entre os correspondentes valores G por locus; a diferença para o valor G observado (G – (A + D)) constitui uma estimativa do valor I para cada classe:
Classes | B–C– | B–cece | bbC– | bbcece |
|---|---|---|---|---|
AX + DX | 0,4 + 9,8 = +10,2 | –46,4 | +5,4 | –51,2 |
GX | +11,8 | –45,2 | +6,8 | –49,2 |
IX | +1,6 | –1,2 | +1,4 | –2,0 |
% de MX | +1,9 | –1,4 | +1,7 | –2,4 |
AY + DY | 0,228 + 0,06 = +0,288 | –0,012 | –0,282 | –0,582 |
GY | +0,328 | –0,172 | –0,342 | –0,342 |
IY | +0,040 | –0,160 | –0,060 | +0,240 |
% de MY | +3,6 | –14,4 | –5,4 | +21,6 |
A comparação entre as variáveis X e Y mostra como a epistasia do genótipo bb para a expressão de Y se traduz num desvio de interacção apreciável, nas classes cece.
Visto que a selecção depende da existência de diferentes valores melhoradores, a variância aditiva, VA, definida como a variância dos valores melhoradores A presentes numa distribuição, é uma medida do potencial avanço dessa selecção. Por referência a M, tem-se
VA = p2(AA1A1)2 + 2pq(AA1A2)2 + q2(AA2A2)2 = 2pqα2
assim como a variância de dominância
VD = p2(DA1A1)2 + 2pq(DA1A2)2 + q2(DA2A2)2 = (2pqd)2
|
Para os mesmos casos particulares:
|
Considerando que não há interacções entre os k loci segregantes, pode escrever-se para qualquer distribuição
![]() e
e![]()
e, dado que COVAD = 0, a variância dos valores genotípicos, VG, define-se como
VG = VA + VD
(assumindo VI = 0)
Exemplo
Voltando ao exemplo da pigmentação do pelo, os dados dos valores de G e I (cf. "valores melhoradores") permitem agora calcular as respectivas variâncias:
Para X:
VG = 0,48×11,82 + 0,16×–45,22 + 0,32×6,82 + 0,08×–49,22 = 602,17
VI = 0,48×1,62 + 0,16×–1,22 + 0,32×1,42 + 0,08×–2,02 = 2,41 (0,4% da VG)
Para Y:
VG = 0,48×0,3282 + 0,16×–0,1722 + 0,32×–0,3422 + 0,08×–0,3422 = 0,10316
VI = 0,48×0,042 + 0,16×–0,162 + 0,32×–0,062 + 0,08×0,242 = 0,01062 (10,3% da VG)
Covariâncias genotípicasConsiderem-se dois indivíduos, P e Q, com as seguintes genealogias:
Se entre eles houver algum parentesco, haverá uma covariância genotípica positiva, a qual (novamente assumindo que não há interacção entre os loci segregando para a característica em estudo) é dada pela fórmula
rVA + uVD
Numa população em equilíbrio de Hardy-Weinberg, r = 2fPQ e u = fACfBD + fADfBC, em que os f são coeficientes de parentesco (cf. "consanguinidade").
Exemplo
Entre irmãos (por exemplo, obtidos a partir de sementes provenientes de um mesmo cruzamento), temos A = C e B = D, donde se obtém (se os progenitores não forem aparentados)
r = 2fPQ = 2 × ¼(fAA + 2fAB + fBB) = 2 × ¼(½ + 0 + ½) = ½
u = fAAfBB + f 2AB = ¼ + 0 = ¼
A tabela seguinte dá os valores de r e de u correspondentes a vários parentescos entre P e Q:
| Tipo de parentesco | Exemplos | r | u |
|---|---|---|---|
| Identidade | mesmo clone | 1 | 1 |
| 1º grau | progenitor (selfing) | 1 | ½ |
um dos progenitores | ½ | 0 | |
irmão | ½ | ¼ | |
| 2º grau | meio-irmão; avô; tio | ¼ | 0 |
primo direito | ¼ | 1/8 | |
| 3º grau | bisavô; meio primo | 1/8 | 0 |
Estes valores (r nomeadamente) são importantes para estimar componentes da variância genotípica em diversas situações (cf. "designs ANOVA")
|
Se se considerarem os valores dos coeficientes de consanguinidade FP e FQ diferentes de 0, então tem-se de dividir 2fPQ pela raiz quadrada dos produtos entre 1 + FP e 1 + FQ: |
Se a interacção entre loci for significativa, considera-se que ela só será importante entre loci dois a dois, definindo-se três componentes da variância de interacção tais que
VI = r2VAA + ruVAD + u2VDD
Referindo-se AA à interacção entre loci homozigóticos, DD entre heterozigóticos, etc.. Note-se que nos parentescos em que u = 0 só VAA contribui:
| Tipo de parentesco | Exemplos | VI |
|---|---|---|
| Identidade | mesmo clone | VAA + VAD + VDD |
| 1º grau | progenitor (selfing) | VAA + ½VAD + ¼VDD |
um dos progenitores | ¼VAA
| |
irmão | ¼VAA + 1/8VAD + 1/16VDD | |
| 2º grau | meio-irmão | 1/16VAA |
Por conseguinte, pelo menos a VAA será de ter em conta quando se suspeita da existência de interacções entre loci. Quanto à ligação cromossómica (que, em tratando-se da segregação de muitos loci, é forçoso que exista), demonstra-se que, na ausência de desequilíbrios de ligação, e na ausência de outras interacções entre os loci ligados, não afecta a fórmula das covariâncias dada acima.
Para que se possa realizar a selecção com expectativas de uma resposta satisfatória, em função dos efeitos médios de substituição αi, é necessário saber qual a interdependência entre os valores fenotípicos P (indicadores de quais os indivíduos a seleccionar), dos indivíduos representados nessa distribuição, e os respectivos valores melhoradores A (indicadores dos reais efeitos a esperar na média da descendência). A medida estatística dessa interdependência (a correlação rAP), tem a seguinte solução algébrica, considerando P = A + NA + E (NA designa "genotípico não-aditivo", isto é, D + I):
Sendo COVAA = VA e admitindo que COVA,NA+E = 0, fica-se com rAP = VA/![]() ,
donde se obtém
,
donde se obtém
O símbolo h2 é conhecido como heritabilidade, e como a fórmula indica define-se como a proporção da variância fenotípica (calculada a partir da distribuição dos fenótipos medidos) que corresponde à variância de valores melhoradores VA. Assim, qualquer variância fenotípica pode ser decomposta em variâncias parcelares atribuíveis às interferências ambientais (VE), aos desvios de dominância e de interacção (VD e VI respectivamente), e finalmente à variância aditiva, VA. Os valores mínimo e máximo para a heritabilidade são 0 e 1, sendo o valor 0 um indicativo de que não há variação nos valores melhoradores, ou seja VA = 0. Qualquer tentativa de selecção com base nos fenótipos só poderá dar resultados (isto é, produzir respostas) se a heritabilidade não for nula. Por isso a determinação da VA numa distribuição fenotípica constitui um passo fundamental para caracterizar geneticamente uma população para o fenótipo em causa.